
【題目】已知 ![]() ,
, ![]() ,函數
,函數 ![]() 的最小值為4.
的最小值為4.
(1)求 ![]() 的值;
的值;
(2)求 ![]() 的最小值.
的最小值.
【答案】
(1)解:因為, ![]() ,
,
所以 ![]() ,當且僅當
,當且僅當 ![]() 時,等號成立,又
時,等號成立,又 ![]() ,
, ![]() ,
,
所以 ![]() ,所以
,所以 ![]() 的最小值為
的最小值為 ![]() ,所以
,所以 ![]() .
.
(2)解:由(1)知 ![]() ,
, ![]() .
.![]()
當且僅當 ![]() ,
, ![]() 時,
時, ![]() 的最小值為
的最小值為 ![]() .
.
【解析】(1)根據絕對值的性質,可得| x + a | + | x b | ≥ | a b | = | a + b | ,所以 ![]() ,當且僅當
,當且僅當 ![]() 時,等號成立,又
時,等號成立,又 ![]() ,
, ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() 的最小值為
的最小值為 ![]() ,所以
,所以 ![]() .
.
(2)因為 a + b = 4 , b = 4 a ,將b參數化掉最后變成一個一元二次方程,就可以求出其最小值.
【考點精析】解答此題的關鍵在于理解復合函數單調性的判斷方法的相關知識,掌握復合函數f[g(x)]的單調性與構成它的函數u=g(x),y=f(u)的單調性密切相關,其規律:“同增異減”,以及對二次函數在閉區間上的最值的理解,了解當![]() 時,當
時,當![]() 時,
時,![]() ;當
;當![]() 時在
時在![]() 上遞減,當
上遞減,當![]() 時,
時,![]() .
.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】編號為 ![]() 的16名籃球運動員在某次訓練比賽中的得分記錄如下:
的16名籃球運動員在某次訓練比賽中的得分記錄如下:
運動員編號 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
運動員編號 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12] | 31 | 38 |
(Ⅰ)將得分在對應區間內的人數填入相應的空格;
區間 |
|
|
|
人數 |
(Ⅱ)從得分在區間 ![]() 內的運動員中隨機抽取2人,
內的運動員中隨機抽取2人,
(i)用運動員的編號列出所有可能的抽取結果;
(ii)求這2人得分之和大于50的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數 ![]() ,
, ![]() ,對于給定的非零實數
,對于給定的非零實數 ![]() ,總存在非零常數
,總存在非零常數 ![]() ,使得定義域
,使得定義域 ![]() 內的任意實數
內的任意實數 ![]() ,都有
,都有 ![]() 恒成立,此時
恒成立,此時 ![]() 為
為 ![]() 的類周期,函數
的類周期,函數 ![]() 是
是 ![]() 上的
上的 ![]() 級類周期函數.若函數
級類周期函數.若函數 ![]() 是定義在區間
是定義在區間 ![]() 內的2級類周期函數,且
內的2級類周期函數,且 ![]() ,當
,當 ![]() 時,
時, 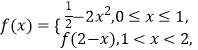 函數
函數 ![]() .若
.若 ![]() ,
, ![]() ,使
,使 ![]() 成立,則實數
成立,則實數 ![]() 的取值范圍是( )
的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+1(a,b為實數,a≠0,x∈R).
(1)若函數f(x)的圖象過點(-2,1),且方程f(x)=0有且只有一個根,求f(x)的表達式;
(2)在(1)的條件下,當x∈[-1,2]時,g(x)=f(x)-kx是單調函數,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐 ![]() 中,底面梯形
中,底面梯形 ![]() ,
, ![]() ,平面
,平面 ![]() 平面
平面 ![]() ,
, ![]() 是等邊三角形,已知
是等邊三角形,已知 ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 上任意一點,
上任意一點, ![]() ,且
,且 ![]() .
.
(1)求證:平面 ![]() 平面
平面 ![]() ;
;
(2)試確定 ![]() 的值,使三棱錐
的值,使三棱錐 ![]() 體積為三棱錐
體積為三棱錐 ![]() 體積的3倍.
體積的3倍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有下面四個命題
p1:若復數z滿足 ![]() ∈R,則z∈R;
∈R,則z∈R;
p2:若復數z滿足z2∈R,則z∈R;
p3:若復數z1 , z2滿足z1z2∈R,則z1= ![]() ;
;
p4:若復數z∈R,則 ![]() ∈R.
∈R.
其中的真命題為( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的三個內角A,B,C的對邊分別a,b,c,已知 ![]() ,
, ![]() ,且
,且 ![]() ∥
∥ ![]()
(1)證明sinBsinC=sinA;
(2)若a2+c2﹣b2= ![]() ac,求tanC.
ac,求tanC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=aln x-bx2 , a,b∈R.
(1)若f(x)在x=1處與直線y=- ![]() 相切,求a,b的值;
相切,求a,b的值;
(2)在(1)的條件下,求f(x)在 ![]() 上的最大值;
上的最大值;
(3)若不等式f(x)≥x對所有的b∈(-∞,0],x∈(e,e2]都成立,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com