
【題目】設函數f(x)=kax﹣a﹣x(a>0且a≠1)是定義域為R的奇函數.
(1)若f(1)>0,試求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值為﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值為﹣2,求m的值.
【答案】
(1)解:∵f(x)是定義域為R的奇函數,∴f(0)=0,可k﹣1=0,即k=1,
故f(x)=ax﹣a﹣x(a>0,且a≠1)
∵f(1)>0,∴a﹣ ![]() >0,又a>0且a≠1,∴a>1.
>0,又a>0且a≠1,∴a>1.
f′(x)=axlna+ ![]()
∵a>1,∴lna>0,而ax+ ![]() >0,
>0,
∴f′(x)>0,∴f(x)在R上單調遞增
原不等式化為:f(x2+2x)>f(4﹣x),
∴x2+2x>4﹣x,即x2+3x﹣4>0
∴x>1或x<﹣4,
∴不等式的解集為{x|x>1或x<﹣4}
(2)解:∵f(1)= ![]() ,∴a﹣
,∴a﹣ ![]() =
= ![]() ,即2a2﹣3a﹣2=0,∴a=2或a=﹣
,即2a2﹣3a﹣2=0,∴a=2或a=﹣ ![]() (舍去).
(舍去).
∴g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.
令t=f(x)=2x﹣2﹣x,由(1)可知f(x)=2x﹣2﹣x為增函數
∵x≥1,∴t≥f(1)= ![]() ,
,
令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2 (t≥ ![]() )
)
若m≥ ![]() ,當t=m時,h(t)min=2﹣m2=﹣2,∴m=2
,當t=m時,h(t)min=2﹣m2=﹣2,∴m=2
若m< ![]() ,當t=
,當t= ![]() 時,h(t)min=
時,h(t)min= ![]() ﹣3m=﹣2,
﹣3m=﹣2,
解得m= ![]() >
> ![]() ,舍去
,舍去
綜上可知m=2
【解析】(1)根據f(x)是定義域為R的奇函數,可得k=1,從而f(x)=ax﹣a﹣x(a>0,且a≠1),利用f(1)>0,可得a>1,從而可證f(x)在R上單調遞增,故原不等式化為x2+2x>4﹣x,從而可求不等式的解集;(2)根據f(1)= ![]() 確定a=2的值,從而可得函數g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.令t=f(x)=2x﹣2﹣x , 由(1)可知f(x)=2x﹣2﹣x為增函數,可得t≥f(1)=
確定a=2的值,從而可得函數g(x)=22x+2﹣2x﹣2m(2x﹣2﹣x)=(2x﹣2﹣x)2﹣2m(2x﹣2﹣x)+2.令t=f(x)=2x﹣2﹣x , 由(1)可知f(x)=2x﹣2﹣x為增函數,可得t≥f(1)= ![]() ,令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2(t≥
,令h(t)=t2﹣2mt+2=(t﹣m)2+2﹣m2(t≥ ![]() ),分類討論,利用最小值為﹣2,可求m的值.
),分類討論,利用最小值為﹣2,可求m的值.
【考點精析】根據題目的已知條件,利用奇偶性與單調性的綜合的相關知識可以得到問題的答案,需要掌握奇函數在關于原點對稱的區間上有相同的單調性;偶函數在關于原點對稱的區間上有相反的單調性.


科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E為CC1的中點,那么異面直線OE與AD1所成角的余弦值等于( ) 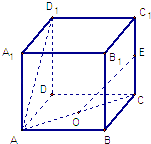
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知P是拋物線y2=8x上的一個動點,Q是圓(x﹣3)2+(y﹣1)2=1上的一個動點,N(2,0)是一個定點,則|PQ|+|PN|的最小值為( )
A.3
B.4
C.5
D.![]() +1
+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某自來水廠的蓄水池存有400噸水,水廠每小時可向蓄水池中注水60噸,同時蓄水池又向居民小區不間斷供水,t小時內供水總量為 ![]() 噸,(0≤t≤24)
噸,(0≤t≤24)
(1)從供水開始到第幾小時時,蓄水池中的存水量最少?最少水量是多少噸?
(2)若蓄水池中水量少于80噸時,就會出現供水緊張現象,請問:在一天的24小時內,有幾小時出現供水緊張現象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2﹣(m﹣1)x+2m
(1)若函數f(x)>0在(0,+∞)上恒成立,求m的取值范圍;
(2)若函數f(x)在(0,1)內有零點,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在[﹣2,2]上的函數y=f(x)和y=g(x),其圖象如圖所示:給出下列四個命題:
①方程f[g(x)]=0有且僅有6個根 ②方程g[f(x)]=0有且僅有3個根
③方程f[f(x)]=0有且僅有5個根 ④方程g[g(x)]=0有且僅有4個根
其中正確命題的序號( )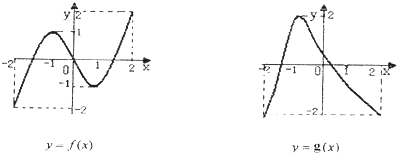
A.①②③
B.②③④
C.①②④
D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ax2﹣(2a+1)x+2lnx(a∈R).
ax2﹣(2a+1)x+2lnx(a∈R).
(1)當a=1時,求函數f(x)的單調區間;
(2)當a>0時,設g(x)=(x2﹣2x)ex , 求證:對任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1的底面是邊長為2的正三角形且側棱垂直于底面,側棱長是 ![]() ,D是AC的中點.
,D是AC的中點. 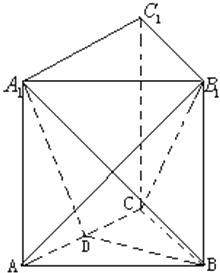
(1)求證:B1C∥平面A1BD;
(2)求二面角A1﹣BD﹣A的大小;
(3)求直線AB1與平面A1BD所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示.
的部分圖象如圖所示.
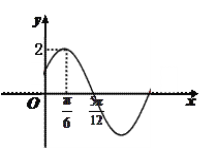
(1) 求函數![]() 的解析式;
的解析式;
(2) 如何由函數![]() 的通過適當圖象的變換得到函數
的通過適當圖象的變換得到函數![]() 的圖象, 寫出變換過程;
的圖象, 寫出變換過程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com