【題目】已知棱長為2的正方體
中，E為DC中點，F在線段
上運動，則三棱錐
的外接球的表面積最小值為（ ）
A.
B.
C.
D.
【答案】C
【解析】
取
的中點
，易知為
的外心，取
的中點
，連接
，取的中點
，連接
，由正方體的性質可得三棱錐
的外接球球心
在直線上，連接
，取
的中點
，連接
、
，易知當
即點
與重合時，即外接球半徑最小，設
，根據
求得
，進而可求得外接球半徑，即可得解.
取的中點，易知為的外心，取的中點，連接，取的中點，連接，
由正方體的性質可得
平面
，
則三棱錐的外接球球心在直線上，連接，
取的中點，連接、，
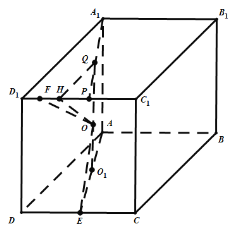
由中位線的性質可得
且
，
所以
，所以
平面
，
，
若要使三棱錐的外接球的表面積最小，則要使其半徑即最小，
易知當即點與重合時，最小，
設，由題意
，
，
則
，
，
由可得
，化簡可得，
此時，三棱錐的外接球的半徑
滿足
，
所以三棱錐的外接球的表面積最小值
.
故選：C.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】山東省2020年高考將實施新的高考改革方案.考生的高考總成績將由3門統一高考科目成績和自主選擇的3門普通高中學業水平等級考試科目成績組成，總分為750分.其中，統一高考科目為語文、數學、外語，自主選擇的3門普通高中學業水平等級考試科目是從物理、化學、生物、歷史、政治、地理6科中選擇3門作為選考科目，語、數、外三科各占150分，選考科目成績采用“賦分制”，即原始分數不直接用，而是按照學生分數在本科目考試的排名來劃分等級并以此打分得到最后得分.根據高考綜合改革方案，將每門等級考試科目中考生的原始成績從高到低分為
、
、
、
、
、
、
、
共8個等級。參照正態分布原則，確定各等級人數所占比例分別為
、
、
、
、、、、.等級考試科目成績計入考生總成績時，將至等級內的考生原始成績，依照等比例轉換法則，分別轉換到91-100、81-90、71-80，61-70、51-60、41-50、31-40、21-30八個分數區間，得到考生的等級成績.
舉例說明.
某同學化學學科原始分為65分，該學科等級的原始分分布區間為58～69，則該同學化學學科的原始成績屬等級.而等級的轉換分區間為61～70，那么該同學化學學科的轉換分為：
設該同學化學科的轉換等級分為
，
，求得
.
四舍五入后該同學化學學科賦分成績為67.
（1）某校高一年級共2000人，為給高一學生合理選科提供依據，對六個選考科目進行測試，其中物理考試原始成績基本服從正態分布
.
（i）若小明同學在這次考試中物理原始分為84分，等級為，其所在原始分分布區間為82～93，求小明轉換后的物理成績；
（ii）求物理原始分在區間
的人數；
（2）按高考改革方案，若從全省考生中隨機抽取4人，記
表示這4人中等級成績在區間
的人數，求的分布列和數學期望.
（附：若隨機變量
，則
，
，
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若實數
滿足
，則稱
為函數
的不動點．
（1）求函數
的不動點；
（2）設函數
，其中
為實數．
① 若
時，存在一個實數
，使得既是
的不動點，又是
的不動點（是函數
的導函數），求實數
的取值范圍；
② 令
，若存在實數
，使，
，
，
成各項都為正數的等比數列，求證：函數
存在不動點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的多面體中，AD⊥平面PDC，四邊形ABCD為平行四邊形，E為AD的中點，F為線段PB上的一點，∠CDP＝120°，AD＝3，AP＝5，
．
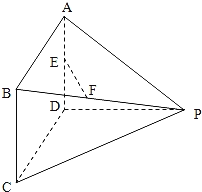
（Ⅰ）試確定點F的位置，使得直線EF∥平面PDC；
（Ⅱ）若PB＝3BF，求直線AF與平面PBC所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了貫徹落實黨中央對新冠肺炎疫情防控工作的部署和要求，堅決防范疫情向校園蔓延，切實保障廣大師生身體健康和生命的安全，教育主管部門決定通過電視頻道、網絡平臺等多種方式實施線上教育教學工作．為了了解學生和家長對網課授課方式的滿意度，從經濟不發達的A城市和經濟發達的B城市分別隨機調查了20個用戶，得到了一個用戶滿意度評分的樣本，并繪制出莖葉圖如下：
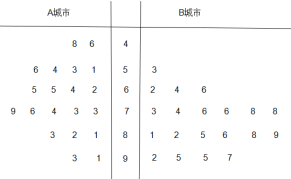
若評分不低于80分，則認為該用戶對此授課方式“認可”，否則認為該用戶對此授課方式“不認可”．以該樣本中A，B城市的用戶對此授課方式“認可”的頻率分別作為A，B城市用戶對此授課方式“認可”的概率．現從A城市和B城市的所有用戶中分別隨機抽取2個用戶，用
表示這4個用戶中對此授課方式“認可”的用戶個數，則
__________；用
表示從A城市隨機抽取2個用戶中對此授課方式“認可”的用戶個數，則的數學期望為_________ ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
