
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)證明:不等式![]() 在
在![]() 恒成立;
恒成立;
(2)證明:![]() 在
在![]() 存在兩個(gè)極值點(diǎn),
存在兩個(gè)極值點(diǎn),
附:![]() ,
,![]() ,
,![]() .
.
【答案】(1)證明見解析;(2)證明見解析;
【解析】
(1)![]() ,首先利用導(dǎo)數(shù)證明當(dāng)
,首先利用導(dǎo)數(shù)證明當(dāng)![]() 時(shí),總有
時(shí),總有![]() ,然后可得
,然后可得![]()
(2)分![]() 和
和![]() 兩種情況討論,每種情況都要用導(dǎo)數(shù)求出
兩種情況討論,每種情況都要用導(dǎo)數(shù)求出![]() 的單調(diào)性.
的單調(diào)性.
(1)![]() ,
,
設(shè)![]() ,易得
,易得![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
又![]() ,
,![]() ,
,
∴存在唯一![]() ,使得
,使得![]() ,
,
∴在![]() 時(shí),
時(shí),![]() ,
,![]() 為減函數(shù),
為減函數(shù),![]() ,
,
在![]() 時(shí),
時(shí),![]() ,
,![]() 為增函數(shù),
為增函數(shù),![]() ,
,
因此![]() 時(shí),總有
時(shí),總有![]() ,
,![]() 為減函數(shù).
為減函數(shù).
∴![]() ,從而原不等式得證.
,從而原不等式得證.
(2)![]() ,則
,則![]() ,
,
在![]() 時(shí),令
時(shí),令![]() ,
,
則![]() 在
在![]() 上遞增.
上遞增.
又![]() ,
,![]() .
.
∴存在唯一![]() ,使
,使![]() .
.
在![]() 時(shí),
時(shí),![]() ,
,![]() 為減函數(shù),即
為減函數(shù),即![]() 為減函數(shù),
為減函數(shù),
在![]() 時(shí),
時(shí),![]() ,
,![]() 為增函數(shù),即
為增函數(shù),即![]() 為增函數(shù),
為增函數(shù),
而![]() ,
,![]() .
.
又![]() ,存在唯一的
,存在唯一的![]() 使得
使得![]() ,
,
∴在![]() 時(shí),
時(shí),![]() ,
,![]() 為減函數(shù),
為減函數(shù),
在![]() 時(shí),
時(shí),![]() ,
,![]() 為增函數(shù),故
為增函數(shù),故![]() 為
為![]() 一個(gè)極小值點(diǎn).
一個(gè)極小值點(diǎn).
另一方面,在![]() 時(shí),由
時(shí),由![]() ,
,
而![]() ,∴
,∴![]() ,
,
由(1)可知![]() ,∴
,∴![]() 在
在![]() 上恒成立,
上恒成立,
又![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 是
是![]() 的極大值點(diǎn),從而得證.
的極大值點(diǎn),從而得證.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)當(dāng)a=-2時(shí),求函數(shù)f(x)的極值;
(2)若ln[e(x+1)]≥2- f(-x)對(duì)任意的x∈[0,+∞)成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知棱長為2的正方體![]() 中,E為DC中點(diǎn),F在線段
中,E為DC中點(diǎn),F在線段![]() 上運(yùn)動(dòng),則三棱錐
上運(yùn)動(dòng),則三棱錐![]() 的外接球的表面積最小值為( )
的外接球的表面積最小值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】農(nóng)歷五月初五是端午節(jié),民間有吃粽子的習(xí)慣,粽子又稱粽粒,俗稱“粽子”,古稱“角黍”,是端午節(jié)大家都會(huì)品嘗的食品,傳說這是為了紀(jì)念戰(zhàn)國時(shí)期楚國大臣、愛國主義詩人屈原.如圖,平行四邊形形狀的紙片是由六個(gè)邊長為2的正三角形構(gòu)成的,將它沿虛線折起來,可以得到如圖所示粽子形狀的六面體,則該六面體的表面積為________;該六面體內(nèi)有一球,則該球體積的最大值為________.
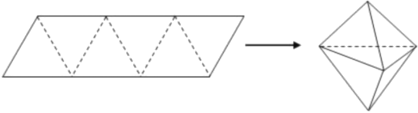
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() ,
,![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)若![]() ,求
,求![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)若![]() 與
與![]() 恰有4個(gè)公共點(diǎn),求
恰有4個(gè)公共點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,其中e是自然對(duì)數(shù)的底數(shù).
,其中e是自然對(duì)數(shù)的底數(shù).
(1)若函數(shù)![]() 的極大值為
的極大值為![]() ,求實(shí)數(shù)a的值;
,求實(shí)數(shù)a的值;
(2)當(dāng)a=e時(shí),若曲線![]() 與
與![]() 在
在![]() 處的切線互相垂直,求
處的切線互相垂直,求![]() 的值;
的值;
(3)設(shè)函數(shù)![]() ,若
,若![]() >0對(duì)任意的x
>0對(duì)任意的x![]() (0,1)恒成立,求實(shí)數(shù)a的取值范圍.
(0,1)恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正項(xiàng)數(shù)列![]() 的首項(xiàng)
的首項(xiàng)![]() ,其前
,其前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() 與
與![]() 的等比中項(xiàng)是
的等比中項(xiàng)是![]() ,數(shù)列
,數(shù)列![]() 滿足:
滿足:![]() .
.
(1)求![]() ,并求數(shù)列
,并求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)記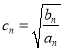 ,
,![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2020年春節(jié)突如其來的新型冠狀病毒肺炎在湖北爆發(fā),一方有難八方支援,全國各地的白衣天使走上戰(zhàn)場(chǎng)的第一線,某醫(yī)院抽調(diào)甲、乙兩名醫(yī)生,抽調(diào)![]() 、
、![]() 、
、![]() 三名護(hù)士支援武漢第一醫(yī)院與第二醫(yī)院,參加武漢疫情狙擊戰(zhàn)其中選一名護(hù)士與一名醫(yī)生去第一醫(yī)院,其它都在第二醫(yī)院工作,則醫(yī)生甲和護(hù)士
三名護(hù)士支援武漢第一醫(yī)院與第二醫(yī)院,參加武漢疫情狙擊戰(zhàn)其中選一名護(hù)士與一名醫(yī)生去第一醫(yī)院,其它都在第二醫(yī)院工作,則醫(yī)生甲和護(hù)士![]() 被選在第一醫(yī)院工作的概率為( )
被選在第一醫(yī)院工作的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,過點(diǎn)
,過點(diǎn)![]() 的直線
的直線![]() 與
與![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)![]() ,且滿足
,且滿足![]() ,以
,以![]() 為中點(diǎn)的線段的兩端點(diǎn)分別為
為中點(diǎn)的線段的兩端點(diǎn)分別為![]() ,其中
,其中![]() 在
在![]() 軸上,
軸上,![]() 在
在![]() 上,則
上,則![]() _______,
_______,![]() 的最小值為____________
的最小值為____________
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com