
如圖所示,圓柱底面的直徑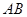 長度為
長度為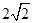 ,
,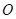 為底面圓心,正三角形
為底面圓心,正三角形 的一個頂點
的一個頂點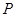 在上底面的圓周上,
在上底面的圓周上,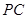 為圓柱的母線,
為圓柱的母線,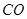 的延長線交
的延長線交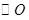 于點
于點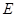 ,
, 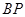 的中點為
的中點為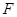 .
.
(1)
求證:平面 ⊥平面
⊥平面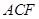 ;
;
(2)
求二面角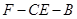 的正切值.
的正切值.
(1)見解析;(2)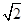 .
.
【解析】本試題主要考查了面面儲值的判定和二面角的求解的綜合運用。
解:(1)證明: 正三角形ABP中,F為BP的中點, ∴AF⊥PB …………1分
∵PC為圓柱的母線, ∴PC⊥平面ABC,
而AC在平面ABC內 ∴PC⊥AC ………………………………2分
∵AB為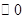 的直徑,∴
的直徑,∴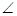 ACB=90°即 AC⊥BC ………………………………3分
ACB=90°即 AC⊥BC ………………………………3分
PC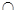 BC=C,∴AC⊥平面PBC,
………………………………………………4分
BC=C,∴AC⊥平面PBC,
………………………………………………4分
而PB在平面PBC內, ∴AC⊥PB ……………………………………5分
AC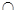 AF=A,∴PB⊥平面ACF,…………………………………………………6分
AF=A,∴PB⊥平面ACF,…………………………………………………6分
而PB在平面ABP內,∴平面ABP⊥平面ACF……………………………………7分
(2) 由(1)知AC⊥BC,PC⊥AC,同理PC⊥BC,
而PA=PB=PC=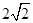 ,可證RT
,可證RT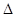 ABC≌RT
ABC≌RT PBC,
PBC,
∴AC=BC=PC=2……8分
以C為原點,CA,CB,CP所在直線為X,Y,Z軸建立空間直角坐標系
則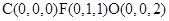 ……………………………9分
……………………………9分
∵PC⊥平面ABC,∴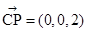 為平面CEB的一個法向量………………10分
為平面CEB的一個法向量………………10分
設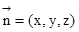 平面CEF的一個法向量,
平面CEF的一個法向量,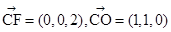
則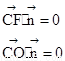 即
即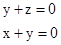 ,令y=-1則
,令y=-1則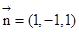 ……………………11分
……………………11分
設二面角F-CE-B的平面角為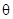 ,
,
∴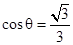 ……………………………………………12分
……………………………………………12分
∴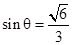 , ……………………………………………………………………13分
, ……………………………………………………………………13分
所以二面角F-CE-B的正切值為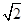 ………………………………………14分
………………………………………14分


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源: 題型:
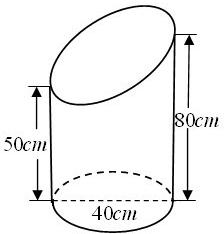
| A、2600cm2 | B、5200cm2 | C、2600πcm2 | D、5200πcm2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•茂名二模)如圖所示,圓柱底面的直徑AB長度為2
(2012•茂名二模)如圖所示,圓柱底面的直徑AB長度為2| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示,圓柱底面的直徑AB長度為2
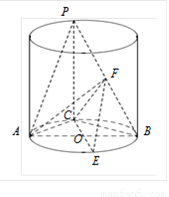
如圖所示,圓柱底面的直徑AB長度為2 ,O為底面圓心,正三角形ABP的一個頂點P在上底面的圓周上,PC為圓柱的母線,CO的延長線交⊙O于點E,BP的中點為F.
,O為底面圓心,正三角形ABP的一個頂點P在上底面的圓周上,PC為圓柱的母線,CO的延長線交⊙O于點E,BP的中點為F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com