
已知橢圓![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,短軸的一個端點到右焦點的距離為
,短軸的一個端點到右焦點的距離為![]() ,直線l:y=kx+m交橢圓于不同的兩點A,B,
,直線l:y=kx+m交橢圓于不同的兩點A,B,
(1)求橢圓的方程,
(2)若坐標原點O到直線l的距離為![]() ,求△AOB面積的最大值.
,求△AOB面積的最大值.
(1)設橢圓的半焦距為c,依題意 ,解得c=
,解得c=![]() .
.
由a2=b2+c2,得b=1.
∴所求橢圓方程為![]() +y2=1.
+y2=1.
(2)由已知得![]() =
=![]() ,可得m2=
,可得m2=![]() (k2+1).
(k2+1).
將y=kx+m代入橢圓方程,
整理得(1+3k2)x2+6kmx+3m2-3=0.
Δ=(6km)2-4(1+3k2)(3m2-3)>0(*)
∴x1+x2=![]() ,x1·x2=
,x1·x2=![]() .
.
∴|AB|2=(1+k2)(x2-x1)2=(1+k2)[![]() -
-![]() ]
]
=![]() =
=![]()
=3+![]() =3+
=3+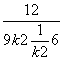 ≤3+
≤3+![]() =4(k≠0),
=4(k≠0),
當且僅當9k2=![]() ,即k=±
,即k=±![]() 時等號成立.
時等號成立.
經檢驗,k=±![]() 滿足(*)式.
滿足(*)式.
當k=0時,|AB|=![]() .
.
綜上可知|AB|max=2.
∴當|AB|最大時,△AOB的面積取最大值Smax=![]() ×2×
×2×![]() =
=![]() .
.


科目:高中數學 來源: 題型:
已知橢圓![]() +
+![]() =1(a>b>0)的一個頂點為A(0,1),離心率為
=1(a>b>0)的一個頂點為A(0,1),離心率為![]() ,
,
過點B(0,-2)及左焦點F1的直線交橢圓于C,D兩點,右焦點設為F2.
(1)求橢圓的方程;
(2)求△CDF2的面積.
查看答案和解析>>
科目:高中數學 來源:2013年全國普通高等學校招生統一考試理科數學(新課標1卷解析版) 題型:選擇題
已知橢圓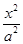 +
+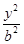 =1(a>b>0)的右焦點為F(3,0),過點F的直線交橢圓于A、B兩點。若AB的中點坐標為(1,-1),則E的方程為 (
)
=1(a>b>0)的右焦點為F(3,0),過點F的直線交橢圓于A、B兩點。若AB的中點坐標為(1,-1),則E的方程為 (
)
A、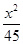 +
+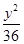 =1
B、
=1
B、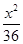 +
+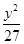 =1
=1
C、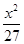 +
+ =1
D、
=1
D、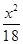 +
+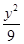 =1
=1
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省濟寧市高三上學期期末模擬文科數學試卷(解析版) 題型:選擇題
設已知橢圓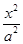 +
+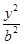 =1(a>b>0)的一個焦點是圓x2+y2-6x+8=0的圓心,且短軸長為8,則橢圓的左頂點為( )
=1(a>b>0)的一個焦點是圓x2+y2-6x+8=0的圓心,且短軸長為8,則橢圓的左頂點為( )
A.(-3,0) B.(-4,0) C.(-10,0) D.(-5,0)
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇省高二9月份質量檢測數學試卷(解析版) 題型:填空題
(本題滿分14分)
已知橢圓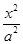 +
+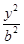 =1(a>b>0)的左右頂點為
=1(a>b>0)的左右頂點為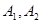 ,上下頂點為
,上下頂點為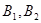 ,
左右焦點為
,
左右焦點為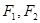 ,若
,若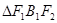 為等腰直角三角形(1)求橢圓的離心率(2)若
為等腰直角三角形(1)求橢圓的離心率(2)若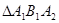 的面積為6
的面積為6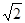 ,求橢圓的方程
,求橢圓的方程
查看答案和解析>>
科目:高中數學 來源:2013屆江西省高二第二次月考文科數學 題型:選擇題
已知橢圓 +
+ =1(a>b>0)的左焦點為F,右頂點為A,點B在橢圓上,且BF⊥x軸,直線AB交y軸于點P.若
=1(a>b>0)的左焦點為F,右頂點為A,點B在橢圓上,且BF⊥x軸,直線AB交y軸于點P.若 =2
=2 ,則橢圓的離心率是( )
,則橢圓的離心率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com