【題目】已知函數
.
（1）若
是
的極值點，試研究函數
的單調性，并求
的極值；
（2）若
在
上恒成立，求實數
的取值范圍.
【答案】（1）詳見解析;（2）
.
【解析】試題分析：（1）現求
，再由
是
的極值點，求得
的值，最后根據
得到函數
的單調性和極值；
（2）將不等式的恒成立問題轉化為求曲線
的最小值問題，對
分類討論，即可確定實數
的取值范圍.
試題解析：
（1）函數
，定義域為
，則
，
若
是
的極值點，則
，即
.
∴
， 
.
令
，則
，令
，則
，
∴
在
上單調遞增，在
上單調遞減，
∴
在
處取得極小值，極小值為
.
（2）若
在
上恒成立，即
.
由（1）知
，
（i）當
時，即
在
上恒成立，即
在
上單調遞減，
則
，得
.
（ii）當
時， 
時， 
，
時， 
，
若
，即
時， 
在
上恒成立，
則
在
上單調遞減，∴
，即
時
恒成立，
若
，即
時， 
時， 
， 
時， 
.
即
在
上單調遞減，在
上單調遞增，
則
，得
.
綜上所述，實數
的取值范圍是
.
科目：高中數學 來源： 題型：
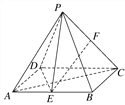
【題目】如圖，四棱錐P－ABCD的底面為矩形，AB＝
，BC＝1，E，F分別是AB，PC的中點，DE⊥PA.
(1)求證：EF∥平面PAD；
(2)求證：平面PAC⊥平面PDE.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝(x＋1)e－x(e為自然對數的底數)．
(1)求函數f(x)的單調區間；
(2)設函數φ(x)＝xf(x)＋tf′(x)＋e－x，存在實數x1，x2∈[0,1]，使得2φ(x1)<φ(x2)成立，求實數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，長方體
中， 
， 
，點
， 
， 
分別為
， 
， 
的中點，過點
的平面
與平面
平行，且與長方體的面相交，交線圍成一個幾何圖形.
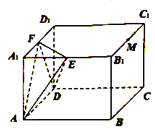
（1）在圖中畫出這個幾何圖形（說明畫法，不需要說明理由）；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已經函數
的定義域為
，設
（1）試確定
的取值范圍，使得函數
在
上為單調函數
（2）求證
（3）若不等式
（為
正整數）對任意正實數
恒成立，求
的最大值.（解答過程可參考使用以下數據
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】把2支相同的晨光簽字筆,3支相同英雄鋼筆全部分給4名優秀學生,每名學生至少1支,則不同的分法有（ ）
A. 24種 B. 28種 C. 32種 D. 36種
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】第三屆移動互聯創新大賽，于2017年3月～10月期間舉行，為了選出優秀選手，某高校先在計算機科學系選出一種子選手
，再從全校征集出3位志愿者分別與
進行一場技術對抗賽，根據以往經驗， 
與這三位志愿者進行比賽一場獲勝的概率分別為
，且各場輸贏互不影響.
（1）求甲恰好獲勝兩場的概率；
（2）求甲獲勝場數的分布列與數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某海產品經銷商調查發現，該海產品每售出
噸可獲利
萬元，每積壓
噸則虧損
萬元.根據往年的數據，得到年需求量的頻率分布直方圖如圖所示，將頻率視為概率.
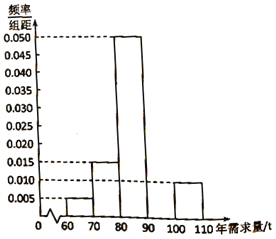
（1）請補齊
上的頻率分布直方圖，并依據該圖估計年需求量的平均數；
（2）今年該經銷商欲進貨
噸，以
（單位：噸， 
）表示今年的年需求量，以
（單位：萬元）表示今年銷售的利潤，試將
表示為
的函數解析式；并求今年的年利潤不少于
萬元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
