
| A. | (1,e) | B. | (e,10] | C. | (1,10] | D. | (10,+∞) |
分析 令g(x)=0得出f(x)=kx,做出y=kx與y=f(x)的函數圖象,則兩圖象有兩個交點,求出y=f(x)的過原點的切線的斜率即可得出k的范圍.
解答 解:令g(x)=0得f(x)=kx,
∵g(x)有兩個零點,
∴直線y=kx與y=f(x)有兩個交點,
做出y=kx和y=f(x)的函數圖象,如圖所示: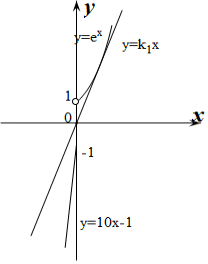
設y=k1x與曲線y=ex相切,切點為(x0,y0),
則$\left\{\begin{array}{l}{{k}_{1}={e}^{{x}_{0}}}\\{{y}_{0}={e}^{{x}_{0}}}\\{{y}_{0}={k}_{1}{x}_{0}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{0}=1}\\{{y}_{0}=e}\\{{k}_{1}=e}\end{array}\right.$.
∵y=kx與y=f(x)有兩個交點,
∴k的取值范圍是(e,10].
故選B.
點評 本題考查了函數零點的個數與函數的圖象的關系,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
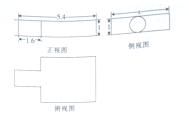 中國古代數學名著《九章算術》中記載了公元前344年商鞅制造一種標準量器-商鞅銅方升,其三視圖(單位:寸)如圖所示,若π取3,其體積為12.6(立方寸),則圖中x的為( )
中國古代數學名著《九章算術》中記載了公元前344年商鞅制造一種標準量器-商鞅銅方升,其三視圖(單位:寸)如圖所示,若π取3,其體積為12.6(立方寸),則圖中x的為( )| A. | 2.5 | B. | 3 | C. | 3.2 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
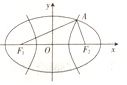 如圖F1,F2是雙曲線${C_1}:{x^2}-\frac{y^2}{8}=1$與橢圓C2的公共焦點,點A是C1,C2在第一象限內的公共點,若|F1F2|=|F1A|,則C2的離心率是( )
如圖F1,F2是雙曲線${C_1}:{x^2}-\frac{y^2}{8}=1$與橢圓C2的公共焦點,點A是C1,C2在第一象限內的公共點,若|F1F2|=|F1A|,則C2的離心率是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1] | B. | [1,2] | C. | [$\frac{2}{3}$,2] | D. | [$\frac{2}{3}$,$\frac{4}{3}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com