【題目】已知函數(shù)
，若方程
有且只有2個不相等的實數(shù)解，則實數(shù)k的取值范圍是______。
【答案】
【解析】
通過分類討論得到
的解析式，通過零點在
或
可求得
的范圍，得
時，
在
上有一個零點；當
時，在上無零點；則討論
時，有一個零點和兩個零點時的取值范圍，綜合
時的結(jié)論，可得結(jié)果.
當時，
當
時，
當
時，
設，則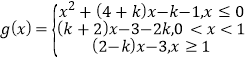
有且只有2個不相等的實數(shù)解等價于有且僅有
個零點
若一個零點位于，即
若一個零點位于，即
可知在，內(nèi)不可能同時存在零點
即當時，在上有一個零點；當時，在上無零點
①當在
上有且僅有一個零點時
⑴當
時，
或
此時在上無零點 
不滿足有兩個零點
⑵當
，即
或
時
只需
，即
時，在上有且僅有一個零點
時，在上有一個零點
時，有且僅有個零點
②當在上有兩個零點時
只需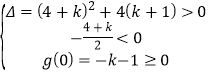
時，在上無零點
時，有且僅有個零點
綜上所述：
狀元及第系列答案
同步奧數(shù)系列答案科目：高中數(shù)學 來源： 題型：
【題目】某貧困地區(qū)扶貧辦積極貫徹落實國家精準扶貧的政策要求，帶領(lǐng)廣大農(nóng)村地區(qū)人民群眾脫貧奔小康.經(jīng)過不懈的奮力拼搏，新農(nóng)村建設取得巨大進步，農(nóng)民年收入也逐年增加，為了更好的制定2019年關(guān)于加快提升農(nóng)民年收入力爭早日脫貧的工作計劃，該地扶貧辦隨機統(tǒng)計了2018年50位農(nóng)民的年收入并制成如下頻率分布直方圖：
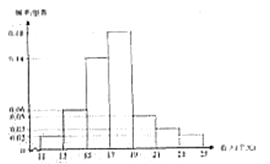
（Ⅰ）根據(jù)頻率分布直方圖，估計50位農(nóng)民的年平均收入
（單位：千元）（同一組數(shù)據(jù)用該組數(shù)據(jù)區(qū)間的中點值表示）；
（Ⅱ）由頻率分布直方圖可認為該貧困地區(qū)農(nóng)民年收入
服從正態(tài)分布
，其中
近似為年平均收入，
近似為樣本方差
，經(jīng)計算得
.利用該正態(tài)分布，求：
（i）在2018年脫貧攻堅工作中，該地區(qū)約有
的農(nóng)民的年收入高于扶貧辦制定的最低年收入標準，則最低年收入大約為多少千元？
（ii）為了調(diào)研“精準扶貧，不落一人”的政策要求落實情況，扶貧辦隨機走訪了1000位農(nóng)民.若每個農(nóng)民的年收入相互獨立，問：這1000位農(nóng)民中的年收入不少于12.14千元的人數(shù)約為多少？
參考數(shù)據(jù)：
.若
，則
；
；
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】為慶祝黨的98歲生日，某高校組織了“歌頌祖國，緊跟黨走”為主題的黨史知識競賽。從參加競賽的學生中，隨機抽取40名學生，將其成績分為六段
，
，
，
，
，
，到如圖所示的頻率分布直方圖.
（1）求圖中
的值及樣本的中位數(shù)與眾數(shù)；
（2）若從競賽成績在與兩個分數(shù)段的學生中隨機選取兩名學生，設這兩名學生的競賽成績之差的絕對值不大于
分為事件
,求事件發(fā)生的概率.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在一場拋擲骰子的游戲中，游戲者最多有三次機會拋擲一顆骰子，游戲規(guī)則如下：拋擲1枚骰子，第1次拋擲骰子向上的點數(shù)為奇數(shù)則記為成功，第2次拋擲骰子向上的點數(shù)為3的倍數(shù)則記為成功，第3次拋擲骰子向上的點數(shù)為6則記為成功.游戲者在前兩次拋擲中至少成功一次才可以進行第三次拋擲，其中拋擲骰子不成功得0分，第1次成功得3分，第2次成功得3分，第3次成功得4分.
（1）求游戲者有機會第3次拋擲骰子的概率；
（2）設游戲者在一場拋擲骰子游戲中所得的分數(shù)為
，求隨機變量的分布列和數(shù)學期望.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知集合
.
（1）求證：函數(shù)
；
（2）某同學由（1）又發(fā)現(xiàn)
是周期函數(shù)且是偶函數(shù)，于是他得出兩個命題：①集合
中的元素都是周期函數(shù)；②集合中的元素都是偶函數(shù)，請對這兩個命題給出判斷，如果正確，請證明；如果不正確，請舉出反例；
（3）設
為非零常數(shù)，求
的充要條件，并給出證明.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知正項數(shù)列
的前
項和為
，且
，
，數(shù)列
滿足
，且
（I）求數(shù)列，的通項公式；
（II）令
，求數(shù)列
的前項和
。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知
是函數(shù)
的極值點.
（Ⅰ）求實數(shù)
的值；
（Ⅱ）求證：函數(shù)
存在唯一的極小值點
，且
.
（參考數(shù)據(jù)：
，
，其中
為自然對數(shù)的底數(shù)）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某省確定從2021年開始，高考采用“
”的模式，取消文理分科，即“3”包括語文、數(shù)學、英語，為必考科目：“1”表示從物理、歷史中任選一門；“2”則是從生物、化學、地理、政治中選擇兩門，共計六門考試科目.某高中從高一年級2000名學生（其中女生900人）中，采用分層抽樣的方法抽取
名學生進行調(diào)查.
（1）已知抽取的名學生中含男生110人，求的值及抽取到的女生人數(shù)；
（2）學校計劃在高二上學期開設選修中的“物理”和“歷史”兩個科目，為了了解學生對這兩個科目的選課情況，對在（1）的條件下抽取到的名學生講行問卷調(diào)查（假定每名學生在這兩個科目中必須選擇一個科目且只能選擇一個科目）.下表是根據(jù)調(diào)查結(jié)果得到的
列聯(lián)表，請將列聯(lián)表補充完整，并判斷是否有
的把握認為選擇科目與性別有關(guān)？說明你的理由；
性別 | 選擇物理 | 選擇歷史 | 總計 |
男生 | 50 | ||
女生 | 30 | ||
總計 |
（3）在（2）的條件下，從抽取的選擇“物理”的學生中按分層抽樣抽取6人，再從這6名學生中抽取2人，對“物理”的選課意向作深入了解，求2人中至少有1名女生的概率.
參考公式：
，其中
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
