【題目】設
，向量
，
，且
.
（1）求點
的軌跡
的方程；
（2）過點
作直線
交曲線于
，
兩點（在
，之間）.設
，直線的傾斜角
，求實數
的取值范圍.
科目：高中數學 來源： 題型：
【題目】已知8支球隊中有3支弱隊，以抽簽方式將這8支球隊分為A、B兩組，每組4支．求：（1）A、B兩組中有一組恰有兩支弱隊的概率；
（2）A組中至少有兩支弱隊的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知0＜m＜2,動點M到兩定點F1（﹣m,0）,F2（m,0）的距離之和為4,設點M的軌跡為曲線C,若曲線C過點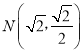
.
（1）求m的值以及曲線C的方程；
（2）過定點
且斜率不為零的直線l與曲線C交于A,B兩點.證明：以AB為直徑的圓過曲線C的右頂點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有4位同學在同一天的上午、下午參加“身高與體重”“立定跳遠”“肺活量”“握力”“臺階”5個項目的測試，每位同學上午、下午各測試1個項目，且不重復.若上午不測“握力”項目，下午不測“臺階”項目，其余項目上午、下午都各測試1人，則不同的安排方式有多少種？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】考察正方體6個面的中心，甲從這6個點中任意選兩個點連成直線，乙也從這6個點中任意選兩個點連成直線，則所得的兩條直線相互平行但不重合的概率等于（ ）.
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，以
，
為頂點作正三角形
，再以
和
的中點
為頂點作正三角形
，再以
和
的中點
為頂點作正三角形
，
，如此繼續下去.有如下結論：
①所作的正三角形的邊長構成公比為
的等比數列；
②每一個正三角形都有一個頂點在直線
上；
③第六個正三角形的不在第五個正三角形邊上的頂點
的坐標是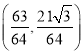
；
④第
個正三角形的不在第
個正三角形邊上的頂點
的橫坐標是
，則
.
其中正確結論的序號是___________.（把你認為正確結論的序號都填上）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知0＜m＜2,動點M到兩定點F1（﹣m,0）,F2（m,0）的距離之和為4,設點M的軌跡為曲線C,若曲線C過點.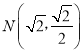
（1）求m的值以及曲線C的方程；
（2）過定點且斜率不為零的直線l與曲線C交于A,B兩點.證明：以AB為直徑的圓過曲線C的右頂點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
的圓心為
，點
是圓內一個定點，點
是圓上任意一點，線段
的重直平分線與半徑
相交于點
．
（1）求動點的軌跡
的方程；
（2）給定點
，若過點
的直線
與軌跡相交于
兩點（均不同于點
）．證明：直線
與直線
的斜率之積為定值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
