
【題目】有4位同學在同一天的上午、下午參加“身高與體重”“立定跳遠”“肺活量”“握力”“臺階”5個項目的測試,每位同學上午、下午各測試1個項目,且不重復.若上午不測“握力”項目,下午不測“臺階”項目,其余項目上午、下午都各測試1人,則不同的安排方式有多少種?
【答案】264種
【解析】
先分別用甲、乙、丙、丁代表四個同學;用1,2,3,4,5代表這5個項目.根據題意,先確定上午的不同安排方式;再結合題意,不妨設上午的安排是:甲1,乙2,丙3,丁5;討論:丁下午測試4,丁下午不測試4兩種情況,分別求出不同的安排方法,進而可求出結果.
分別用甲、乙、丙、丁代表四個同學;用1,2,3,4,5代表這5個項目.
由條件,上午的安排是1,2,3,5的排列,共有![]() 種;
種;
由于每位同學上午、下午各測試1個項目,且不重復,故下午的安排是1,2,3,4的排列,但不允許出現某同學上午、下午測試同一項目的情況.
不妨設上午的安排是:甲1,乙2,丙3,丁5;
(1)若丁下午測試4,則甲乙丙測試的項目可以為:2,3,1;3,1,2;共2種;
(2)當丁下午不測試4,則丁有![]() 種選擇,需從甲乙丙中選擇1人測試4,則有
種選擇,需從甲乙丙中選擇1人測試4,則有![]() 種選擇;剩下兩人只有1種選擇;
種選擇;剩下兩人只有1種選擇;
故下午不同的安排方式有![]() 種;
種;
所以,共有![]() 種不同的安排方式.
種不同的安排方式.


科目:高中數學 來源: 題型:
【題目】對任意實數![]() 給出下列命題:①“
給出下列命題:①“![]() ”是“
”是“![]() ”的充要條件;②“
”的充要條件;②“![]() 是無理數”是“
是無理數”是“![]() 是無理數”的充要條件;③“
是無理數”的充要條件;③“![]() ”是“
”是“![]() ”的充分條件;④“
”的充分條件;④“![]() ”是“
”是“![]() ”的必要條件.其中真命題的個數是( )
”的必要條件.其中真命題的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司對旗下的甲、乙兩個門店在1至9月份的營業額(單位:萬元)進行統計并得到如圖折線圖.

下面關于兩個門店營業額的分析中,錯誤的是( )
A.甲門店的營業額折線圖具有較好的對稱性,故而營業額的平均值約為32萬元
B.根據甲門店的營業額折線圖可知,該門店營業額的平均值在[20,25]內
C.根據乙門店的營業額折線圖可知,其營業額總體是上升趨勢
D.乙門店在這9個月份中的營業額的極差為25萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別是a,b,c,已知sinC+cosC=1-sin![]() .
.
(1)求sinC的值;
(2)若a2+b2=4(a+b)-8,求邊c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某課程考核分理論與實驗兩部分進行,每部分考核成績只記“合格”與“不合格”,兩部分考核都是“合格”,則該課程考核“合格”,若甲、乙、丙三人在理論考核中合格的概率分別為0.9,0.8,0.7,在實驗考核中合格的概率分別為0.8,0.7,0.9,所有考核是否合格相互之間沒有影響.
(1)求甲、乙、丙三人在理論考核中至少有兩人合格的概率;
(2)求這三個人該課程考核都合格的概率(結果保留三位小數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】兩城市![]() 和
和![]() 相距
相距![]() ,現計劃在兩城市外以
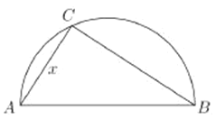
,現計劃在兩城市外以![]() 為直徑的半圓
為直徑的半圓![]() 上選擇一點
上選擇一點![]() 建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關,對城
建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關,對城![]() 和城
和城![]() 的總影響度為城
的總影響度為城![]() 和城
和城![]() 的影響度之和,記
的影響度之和,記![]() 點到城
點到城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理場對城
處的垃圾處理場對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() ,統計調查表明:垃圾處理場對城
,統計調查表明:垃圾處理場對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數為4,對城
的距離的平方成反比,比例系數為4,對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數為
的距離的平方成反比,比例系數為![]() ,當垃圾處理場建在
,當垃圾處理場建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065;
的總影響度為0.065;
(1)將![]() 表示成
表示成![]() 的函數;
的函數;
(2)判斷![]() 上是否存在一點,使建在此處的垃圾處理場對城
上是否存在一點,使建在此處的垃圾處理場對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,說明理由;
的距離;若不存在,說明理由;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com