
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數,且
上的奇函數,且![]() ,對任意的
,對任意的![]()
![]() 且
且![]() 時,有
時,有![]() 成立.
成立.
(1)判斷![]() 在
在![]() 上的單調性,并用定義證明;
上的單調性,并用定義證明;
(2)解不等式![]() ;
;
(3)若![]() 對任意的
對任意的![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用函數單調性的定義,結合函數![]() 為奇函數以及題目所給已知條件,證得
為奇函數以及題目所給已知條件,證得![]() ,由此判斷出函數
,由此判斷出函數![]() 在
在![]() 上遞增.(2)根據函數的定義域和單調性列不等式組,解不等式組求得不等式的解集.(3)根據
上遞增.(2)根據函數的定義域和單調性列不等式組,解不等式組求得不等式的解集.(3)根據![]() 的單調性,將問題轉化為
的單調性,將問題轉化為![]() ,對
,對![]() 恒成立問題來求解,構造函數
恒成立問題來求解,構造函數![]() ,結合一次函數的性質列不等式,解不等式求得
,結合一次函數的性質列不等式,解不等式求得![]() 的取值范圍.
的取值范圍.
(1)證明任取![]() 且
且![]() ,則
,則![]() ,
,
∵![]() 為奇函數,∴
為奇函數,∴![]() ,
,
∴![]()
由已知得![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
(2)∵![]() 在
在![]() 上單調遞增,∴
上單調遞增,∴ ,解得
,解得![]() .
.
![]() 不等式的解集為
不等式的解集為![]()
(3)∵![]() ,
,![]() 在
在![]() 上單調遞增,∴在
上單調遞增,∴在![]() 上,
上,![]() .
.
問題轉化為![]() ,即
,即![]() ,對
,對![]() 恒成立.
恒成立.
設![]() .
.
①若![]() ,則
,則![]() ,對
,對![]() 恒成立.
恒成立.
②若![]() ,則
,則![]() 為
為![]() 的一次函數,若
的一次函數,若![]() ,對
,對![]() 恒成立,必須
恒成立,必須![]() ,且
,且![]() ,∴
,∴![]() 或
或![]() .
.
∴![]() 的取值范圍是
的取值范圍是![]() 或
或![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】一個商場經銷某種商品,根據以往資料統計,每位顧客采用的分期付款次數![]() 的分布列為:
的分布列為:
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商場經銷一件該商品,采用1期付款,其利潤為200元;采用2期或3期付款,其利潤為250元;采用4期或5期付款,其利潤為300元.![]() 表示經銷一件該商品的利潤.
表示經銷一件該商品的利潤.
(1)求購買該商品的3位顧客中,恰有2位采用1期付款的概率;
(2)求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosωx﹣sinωx,sinωx),
=(cosωx﹣sinωx,sinωx), ![]() =(﹣cosωx﹣sinωx,2
=(﹣cosωx﹣sinωx,2 ![]() cosωx),設函數f(x)=
cosωx),設函數f(x)= ![]()
![]() +λ(x∈R)的圖象關于直線x=π對稱,其中ω,λ為常數,且ω∈(
+λ(x∈R)的圖象關于直線x=π對稱,其中ω,λ為常數,且ω∈( ![]() ,1)
,1)
(1)求函數f(x)的最小正周期;
(2)若y=f(x)的圖象經過點( ![]() ,0)求函數f(x)在區間[0,
,0)求函數f(x)在區間[0, ![]() ]上的取值范圍.
]上的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】五個人站成一排,求在下列條件下的不同排法種數:
(1)甲必須在排頭;
(2)甲、乙相鄰;
(3)甲不在排頭,并且乙不在排尾;
(4)其中甲、乙兩人自左向右從高到矮排列且互不相鄰
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為某班35名學生的投籃成績(每人投一次)的條形統計圖,其中上面部分數據破損導致數據不完全。已知該班學生投籃成績的中位數是5,則根據統計圖,則下列說法錯誤的是( )

A. 3球以下(含3球)的人數為10
B. 4球以下(含4球)的人數為17
C. 5球以下(含5球)的人數無法確定
D. 5球的人數和6球的人數一樣多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分別是AC,AB上的點,且DE∥BC,DE=2,將△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如圖2.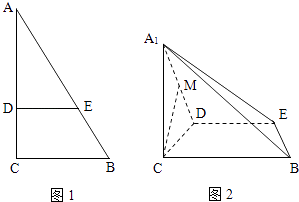
(1)求證:A1C⊥平面BCDE;
(2)若M是A1D的中點,求CM與平面A1BE所成角的大小;
(3)線段BC上是否存在點P,使平面A1DP與平面A1BE垂直?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com