
【題目】如圖,在![]() 中,
中, ![]() ,四邊形
,四邊形![]() 是邊長為
是邊長為![]() 的正方形,平面
的正方形,平面![]() 平面
平面![]() ,若
,若![]() ,
, ![]() 分別是
分別是![]() 的中點.
的中點.
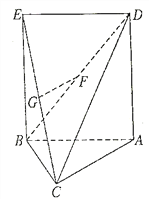
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)求幾何體![]() 的體和
的體和![]() .
.
【答案】(1)詳見解析(2)詳見解析(2)![]()
【解析】試題分析:(1)如圖,連接EA交BD于F,利用正方形的性質、三角形的中位線定理、線面平行的判定定理即可證明.(2)利用已知可得:FG⊥平面EBC,可得∠FBG就是線BD與平面EBC所成的角.經過計算即可得出.(3)利用VEFBC=VFEBC=![]() S△EBCFG即可得出.
S△EBCFG即可得出.
試題解析:
(1)如圖,連接![]() ,易知
,易知![]() 為
為![]() 的中點.
的中點.
因為![]() ,
, ![]() 分別是
分別是![]() 和
和![]() 的中點,
的中點,
所以![]() ,
,
因為![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)證明:因為四邊形![]() 為正方形,
為正方形,
所以![]() .
.
又因為平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .所以
.所以![]() .
.
又因為![]() ,所以
,所以![]() .
.
所以![]() 平面
平面![]() .從而平面
.從而平面![]() 平面
平面![]() .
.
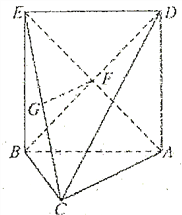
(3)如(1)證法二中的圖,連接![]() ,因為
,因為![]() ,
,
所以![]() ,且
,且![]() .
.
又平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因為![]() 是四棱錐,
是四棱錐,
所以![]() .
.
即幾何體![]() 的體積
的體積![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)解不等式![]() ;
;
(2)若函數![]() 在區間
在區間![]() 上存在零點,求實數
上存在零點,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,其中
,其中![]() 為奇函數,
為奇函數, ![]() 為偶函數,若不等式
為偶函數,若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某生態園將一三角形地塊ABC的一角APQ開辟為水果園種植桃樹,已知角A為120°,AB,AC的長度均大于200米,現在邊界AP,AQ處建圍墻,在PQ處圍竹籬笆. 
(1)若圍墻AP,AQ總長度為200米,如何圍可使得三角形地塊APQ的面積最大?
(2)已知AP段圍墻高1米,AQ段圍墻高1.5米,AP段圍墻造價為每平方米150元,AQ段圍墻造價為每平方米100元.若圍圍墻用了30000元,問如何圍可使竹籬笆用料最省?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lnx﹣ax,a∈R.
(1)當x=1時,函數f(x)取得極值,求a的值;
(2)當0<a< ![]() 時,求函數f(x)在區間[1,2]上的最大值;
時,求函數f(x)在區間[1,2]上的最大值;
(3)當a=﹣1時,關于x的方程2mf(x)=x2(m>0)有唯一實數解,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數h(x)=(m2﹣5m+1)xm+1為冪函數,且為奇函數.
(1)求m的值;
(2)求函數g(x)=h(x)+ ![]() 在x∈[0,
在x∈[0, ![]() ]的值域.
]的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com