
【題目】在平面直角坐標系![]() 中取兩個定點
中取兩個定點![]() ,
,![]() ,再取兩個動點
,再取兩個動點![]() ,
,![]() ,且
,且![]() .
.
(1)求直線![]() 與
與![]() 的交點
的交點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過![]() 的直線與軌跡
的直線與軌跡![]() 交于
交于![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸且與軌跡
軸且與軌跡![]() 交于另一點
交于另一點![]() ,
,![]() 為軌跡
為軌跡![]() 的右焦點,若
的右焦點,若![]() ,求證:
,求證:![]()
科目:高中數學 來源: 題型:
【題目】某校進行了一次創新作文大賽,共有100名同學參賽,經過評判,這100名參賽者的得分都在![]() 之間,其得分的頻率分布直方圖如圖,則下列結論錯誤的是( )
之間,其得分的頻率分布直方圖如圖,則下列結論錯誤的是( )
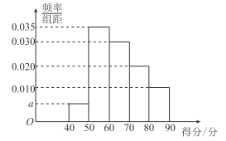
A.得分在![]() 之間的共有40人
之間的共有40人
B.從這100名參賽者中隨機選取1人,其得分在![]() 的概率為0.5
的概率為0.5
C.估計得分的眾數為55
D.這100名參賽者得分的中位數為65
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某客戶考察了一款熱銷的凈水器,使用壽命為十年,改款凈水器為三級過濾,每一級過濾都由核心部件濾芯來實現.在使用過程中,一級濾芯需要不定期更換,其中每更換![]() 個一級濾芯就需要更換
個一級濾芯就需要更換![]() 個二級濾芯,三級濾芯無需更換.其中一級濾芯每個
個二級濾芯,三級濾芯無需更換.其中一級濾芯每個![]() 元,二級濾芯每個
元,二級濾芯每個![]() 元.記一臺凈水器在使用期內需要更換的二級濾芯的個數構成的集合為
元.記一臺凈水器在使用期內需要更換的二級濾芯的個數構成的集合為![]() .如圖是根據
.如圖是根據![]() 臺該款凈水器在十年使用期內更換的一級濾芯的個數制成的柱狀圖.
臺該款凈水器在十年使用期內更換的一級濾芯的個數制成的柱狀圖.
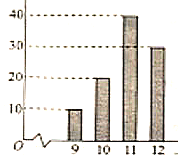
(1)結合圖,寫出集合![]() ;
;
(2)根據以上信息,求出一臺凈水器在使用期內更換二級濾芯的費用大于![]() 元的概率(以
元的概率(以![]() 臺凈水器更換二級濾芯的頻率代替
臺凈水器更換二級濾芯的頻率代替![]() 臺凈水器更換二級濾芯發生的概率);
臺凈水器更換二級濾芯發生的概率);
(3)若在購買凈水器的同時購買濾芯,則濾芯可享受![]() 折優惠(使用過程中如需再購買無優惠).假設上述
折優惠(使用過程中如需再購買無優惠).假設上述![]() 臺凈水器在購機的同時,每臺均購買
臺凈水器在購機的同時,每臺均購買![]() 個一級濾芯、
個一級濾芯、![]() 個二級濾芯作為備用濾芯(其中
個二級濾芯作為備用濾芯(其中![]() ,
,![]() ),計算這
),計算這![]() 臺凈水器在使用期內購買濾芯所需總費用的平均數.并以此作為決策依據,如果客戶購買凈水器的同時購買備用濾芯的總數也為
臺凈水器在使用期內購買濾芯所需總費用的平均數.并以此作為決策依據,如果客戶購買凈水器的同時購買備用濾芯的總數也為![]() 個,則其中一級濾芯和二級濾芯的個數應分別是多少?
個,則其中一級濾芯和二級濾芯的個數應分別是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,曲線![]() 的參數方程為
的參數方程為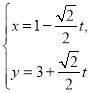 (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出![]() 的普通方程及
的普通方程及![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,求
上,求![]() 的最小值及此時點
的最小值及此時點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉行運動會,其中三級跳遠的成績在![]() 米以上的進入決賽,把所得的成績進行整理后,分成
米以上的進入決賽,把所得的成績進行整理后,分成![]() 組畫出頻率分布直方圖的一部分(如圖),已知第
組畫出頻率分布直方圖的一部分(如圖),已知第![]() 組的頻數是
組的頻數是![]() .
.
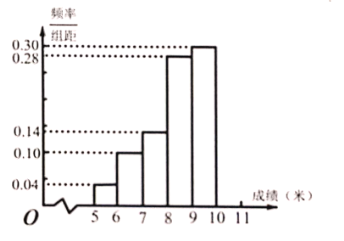
(1)求進入決賽的人數;
(2)用樣本的頻率代替概率,記![]() 表示兩人中進入決賽的人數,求
表示兩人中進入決賽的人數,求![]() 得分布列及數學期望.
得分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某校學生參加社區服務的情況,采用按性別分層抽樣的方法進行調查.已知該校共有學生960人,其中男生560人,從全校學生中抽取了容量為n的樣本,得到一周參加社區服務時間的統計數據如下:
超過1小時 | 不超過1小時 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95%的把握認為該校學生一周參加社區服務時間是否超過1小時與性別有關?
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《周髀算經》中給出了勾股定理的絕妙證明.如圖是趙爽弦圖及注文.弦圖是一個以勾股形之弦為邊的正方形,其面積稱為弦實.圖中包含四個全等的勾股形及一個小正方形,分別涂成朱色及黃色,其面積稱為朱實、黃實.由2×勾×股+(股-勾)2=4×朱實+黃實=弦實,化簡得勾2+股2=弦2.若圖中勾股形的勾股比為![]() ,向弦圖內隨機拋擲100顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘顆數大約為( )(參考數據:
,向弦圖內隨機拋擲100顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘顆數大約為( )(參考數據:![]() ,
,![]() )
)
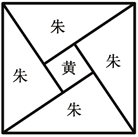
A.2B.4C.6D.8
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,
為矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值;
所成銳二面角的余弦值;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出線段
,若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() .過焦點且垂直于
.過焦點且垂直于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 相交所得的弦長為3,直線
相交所得的弦長為3,直線![]() 與橢圓
與橢圓![]() 相切.
相切.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)是否存在直線![]() :
:![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,使得
兩點,使得![]() ?若存在,求
?若存在,求![]() 的取值范圍;若不存在,請說明理由!
的取值范圍;若不存在,請說明理由!
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com