（滿分14分）
對于在區間A上有意義的兩個函數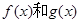
，如果對任意的
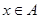，恒有
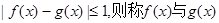在A上是接近的，否則稱
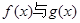在A上是非接近的。
（1）證明：函數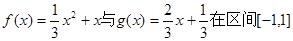
上是接近的；
（2）若函數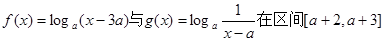
上是接近的，求實數a的取值范圍。
高中必刷題系列答案科目：高中數學 來源：2011-2012學年廣東省翠園中學高二上學期期中考試理科數學 題型：解答題
（本題滿分14分）.對某電子元件進行壽命追蹤調查，情況如下.
| 壽命（h） | 100～200 | 200～300 | 300～400 | 400～500 | 500～600 |
| 個 數 | 20 | 30 | 80 | 40 | 30 |
查看答案和解析>>
科目：高中數學 來源：2012-2013學年湖南省元月考文科數學試卷（解析版） 題型：解答題
（本小題滿分14分）對定義域分別是
、
的函數
、
，
規定：函數
已知函數
，
．
（1）求函數
的解析式；
⑵對于實數
，函數是否存在最小值，如果存在，求出其最小值；如果不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源：2014屆廣東省高一下學期期中考試數學試卷（解析版） 題型：解答題
（本小題滿分14分）
對甲、乙的學習成績進行抽樣分析，各抽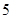
門功課，得到的觀測值如下： 
問：甲、乙誰的平均成績較好？誰的各門功課發展較平衡？
查看答案和解析>>
科目：高中數學 來源：2011年四川省成都市畢業班摸底測試（文科）數學卷 題型：解答題
（本小題滿分14分） 對函數Φ（x），定義fk（x）＝Φ（x－mk）＋nk（其中x∈（mk，
m＋mk]，k∈Z，m＞0，n＞0，且m、n為常數）為Φ（x）的第k階階梯函數，m叫做階寬，n叫做階高，已知階寬為2，階高為3．
（1）當Φ（x）＝2x時 ①求f0（x）和fk（x）的解析式； ②求證：Φ（x）的各階階梯函數圖象的最高點共線；
查看答案和解析>>
科目：高中數學 來源：2010年內蒙古元寶山區高三第一次摸底考試理科數學卷 題型：解答題
（本小題滿分14分） 對函數Φ（x），定義fk（x）＝Φ（x－mk）＋nk（其中x∈（mk，
m＋mk]，k∈Z，m＞0，n＞0，且m、n為常數）為Φ（x）的第k階階梯函數，m叫做階寬，n叫做階高，已知階寬為2，階高為3．
（1）當Φ（x）＝2x時 ①求f0（x）和fk（x）的解析式； ②求證：Φ（x）的各階階梯函數圖象的最高點共線；
（2）若Φ（x）＝x2，則是否存在正整數k，使得不等式fk（x）＜（1－3k）x＋4k2＋3k－1有解？若存在，求出k的值；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
上是接近的 ………………4分
，恒有
…………8分
…………14分
