
【題目】已知函數f(x)=2sinxcos(x-![]() ).
).
(Ⅰ)求函數f(x)的最小正周期.
(Ⅱ)當x∈[0, ![]() ]時,求函數f(x)的取值范圍.
]時,求函數f(x)的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)f(x)∈[0,1+
;(Ⅱ)f(x)∈[0,1+![]() ].
].
【解析】試題分析:(Ⅰ)由兩角差的余弦公式展開,結合二倍角公式化簡得f(x)=sin(2x-![]() )+
)+![]() ,進而得周期;
,進而得周期;
(Ⅱ)由x∈[0, ![]() ]得2x-
]得2x-![]() ∈[-
∈[-![]() ,
,![]() ],即可得sin(2x-
],即可得sin(2x-![]() )∈[-
)∈[-![]() ,1],從而得解.
,1],從而得解.
試題解析:
因為f(x)=2sinx×cos(x-![]() ),
),
所以f(x)=2sinx×(cosxcos![]() +sinxsin
+sinxsin![]() )=sinx×cosx+
)=sinx×cosx+![]() sin2x=
sin2x=![]() sin2x+
sin2x+![]() (1-cos2x)=sin(2x-
(1-cos2x)=sin(2x-![]() )+
)+![]() .
.
(Ⅰ)函數f(x)的最小正周期為![]() .
.
(Ⅱ)因為x∈[0, ![]() ],所以2x-
],所以2x-![]() ∈[-
∈[-![]() ,
,![]() ].
].
所以sin(2x-![]() )∈[-
)∈[-![]() ,1].
,1].
所以f(x)∈[0,1+![]() ].
].


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】以A表示值域為R的函數組成的集合,B表示具有如下性質的函數![]() 組成的集合:對于函數
組成的集合:對于函數![]() ,存在一個正數M,使得函數
,存在一個正數M,使得函數![]() 的值域包含于區間[-M,M]。例如,當
的值域包含于區間[-M,M]。例如,當![]() ,
, ![]() 時,
時, ![]() ,現有如下命題:
,現有如下命題:
①設函數![]() 的定義域為D,則“
的定義域為D,則“![]() ”的充要條件是“
”的充要條件是“![]() ”;
”;
②若函數![]() ,則
,則![]() 有最大值和最小值;
有最大值和最小值;
③若函數![]() ,
, ![]() 的定義域相同,且
的定義域相同,且![]() ,
, ![]() ,則
,則![]()
④若函數![]() ,則
,則![]() 有最大值且
有最大值且![]() ,
,
其中的真命題有_____________。(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲,乙,丙,丁四名同學做傳遞手帕游戲(每位同學傳遞到另一位同學記傳遞1次),手帕從甲手中開始傳遞,經過5次傳遞后手帕回到甲手中,則共有__________種不同的傳遞方法.(用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設滿足以下兩個條件的有窮數列![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 階“期待數列”:
階“期待數列”:
①![]() ;
;
②![]() .
.
(![]() )分別寫出一個單調遞增的
)分別寫出一個單調遞增的![]() 階和
階和![]() 階“期待數列”.
階“期待數列”.
(![]() )若某
)若某![]() 階“期待數列”是等差數列,求該數列的通項公式.
階“期待數列”是等差數列,求該數列的通項公式.
(![]() )記
)記![]() 階“期待數列”的前
階“期待數列”的前![]() 項和為
項和為![]() ,試證:
,試證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為減少汽車尾氣排放,提高空氣質量,各地紛紛推出汽車尾號限行措施.為做好此項工作,某市交警支隊對市區各交通樞紐進行調查統計,表中列出了某交通路口單位時間內通過的1000輛汽車的車牌尾號記錄:
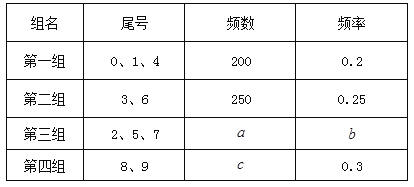
由于某些數據缺失,表中以英文字母作標識.請根據圖表提供的信息計算:
(Ⅰ)若采用分層抽樣的方法從這1000輛汽車中抽出20輛,了解駕駛員對尾號限行的建議,應分別從一、二、三、四組中各抽取多少輛?
(Ⅱ)以頻率代替概率,在此路口隨機抽取4輛汽車,獎勵汽車用品.用![]() 表示車尾號在第二組的汽車數目,求
表示車尾號在第二組的汽車數目,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
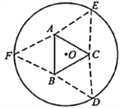
【題目】如圖,圓形紙片的圓心為O,半徑為5 cm,該紙片上的等邊三角形ABC的中心為O.D、E、F為圓O上的點,△DBC,△ECA,△FAB分別是以BC,CA,AB為底邊的等腰三角形.沿虛線剪開后,分別以BC,CA,AB為折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱錐.當△ABC的邊長變化時,所得三棱錐體積(單位:cm3)的最大值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
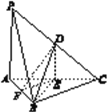
【題目】如圖,在三棱錐P-ABC中,D,E,F分別為PC,AC,AB的中點.已知PA⊥AC,PA=6,BC=8,DF=5.
求證:(1)直線PA∥平面DEF;
(2)平面BDE⊥平面ABC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com