
【題目】中國乒乓球隊備戰里約奧運會熱身賽暨選撥賽于2016年7月14日在山東威海開賽,種子選手A與非種子選手B1 , B2 , B3分別進行一場對抗賽,按以往多次比賽的統計,A獲勝的概率分別為 ![]() ,且各場比賽互不影響.
,且各場比賽互不影響.
(Ⅰ)若A至少獲勝兩場的概率大于 ![]() ,則A入選征戰里約奧運會的最終名單,否則不予入選,問A是否會入選最終的名單?
,則A入選征戰里約奧運會的最終名單,否則不予入選,問A是否會入選最終的名單?
(Ⅱ)求A獲勝場數X的分布列和數學期望.
【答案】解:(Ⅰ)記“種子A與非種子B1、B2、B3比賽獲勝”分別為事件A1、A2、A3![]()
![]() =
= ![]()
所以,A入選最終名單….6
(Ⅱ)X的可能值為0、1、2、3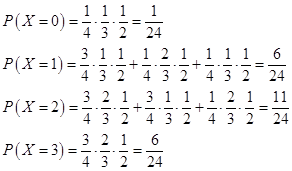
所以,X的分布列為
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以,數學期望: ![]()
【解析】(Ⅰ)利用相互獨立事件的概率公式,結合條件,即可求解;(Ⅱ)據題意,X的可能值為0、1、2、3,求出概率,列出分布列,然后求解期望.
【考點精析】利用離散型隨機變量及其分布列對題目進行判斷即可得到答案,需要熟知在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


科目:高中數學 來源: 題型:
【題目】(本題滿分12分)若點![]() ,在
,在![]() 中按均勻分布出現.
中按均勻分布出現.
(1)點![]() 橫、縱坐標分別由擲骰子確定,第一次確定橫坐標,第二次確定縱坐標,則點
橫、縱坐標分別由擲骰子確定,第一次確定橫坐標,第二次確定縱坐標,則點![]() 落在上述區域的概率?
落在上述區域的概率?
(2)試求方程![]() 有兩個實數根的概率.
有兩個實數根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程為 ![]() (α為參數),以直角坐標系原點為極點,Ox軸正半軸為極軸建立極坐標系.
(α為參數),以直角坐標系原點為極點,Ox軸正半軸為極軸建立極坐標系.
(1)求曲線C的極坐標方程
(2)若直線l的極坐標方程為ρ(sinθ+cosθ)=1,求直線l被曲線C截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】奧地利遺傳學家孟德爾1856年用豌豆作實驗時,他選擇了兩種性狀不同的豌豆,一種是子葉顏色為黃色,種子性狀為圓形,莖的高度為長莖,另一種是子葉顏色為綠色,種子性狀為皺皮,莖的高度為短莖。我們把純黃色的豌豆種子的兩個特征記作![]() ,把純綠色的豌豆的種子的兩個特征記作
,把純綠色的豌豆的種子的兩個特征記作![]() ,實驗雜交第一代收獲的豌豆記作
,實驗雜交第一代收獲的豌豆記作![]() ,第二代收獲的豌豆出現了三種特征分別為
,第二代收獲的豌豆出現了三種特征分別為![]() ,
,![]() ,
,![]() ,請問,孟德爾豌豆實驗第二代收獲的有特征
,請問,孟德爾豌豆實驗第二代收獲的有特征![]() 的豌豆數量占總收成的( )
的豌豆數量占總收成的( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在框圖中,設x=2,并在輸入框中輸入n=4;ai=i(i=0,1,2,3,4).則此程序執行后輸出的S值為( )

A. 26 B. 49 C. 52 D. 98
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:噸)的影響,對近六年的年宣傳費
(單位:噸)的影響,對近六年的年宣傳費![]() 和年銷售量
和年銷售量![]() (
(![]() )的數據作了初步統計,得到如下數據:
)的數據作了初步統計,得到如下數據:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年宣傳費 | 23 | 25 | 27 | 29 | 32 | 35 |
年銷售量 | 11 | 21 | 24 | 66 | 115 | 325 |
(1)根據散點圖判斷![]() 與
與![]() ,哪一個更適合作為年銷售量
,哪一個更適合作為年銷售量![]() (噸)與關于宣傳費
(噸)與關于宣傳費![]() (萬元)的回歸方程類型;
(萬元)的回歸方程類型;
(2)規定當產品的年銷售量![]() (噸)與年宣傳費
(噸)與年宣傳費![]() (萬元)的比值大于1時,認為該年效益良好,現從這6年中任選3年,記其中選到效益良好的數量為
(萬元)的比值大于1時,認為該年效益良好,現從這6年中任選3年,記其中選到效益良好的數量為![]() ,試求
,試求![]() 的所有取值情況及對應的概率;
的所有取值情況及對應的概率;
(3)根據頻率分布直方圖中求出樣本數據平均數的思想方法,求![]() 的平均數.
的平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
: ![]() 過圓上任意一點
過圓上任意一點![]() 向
向![]() 軸引垂線垂足為
軸引垂線垂足為![]() (點
(點![]() 、
、![]() 可重合),點
可重合),點![]() 為
為![]() 的中點.
的中點.
(1)求![]() 的軌跡方程;
的軌跡方程;
(2)若點![]() 的軌跡方程為曲線
的軌跡方程為曲線![]() ,不過原點
,不過原點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,滿足直線
兩點,滿足直線![]() ,
, ![]() ,
, ![]() 的斜率依次成等比數列,求
的斜率依次成等比數列,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直線![]() 與圓
與圓 ![]() 且與橢圓
且與橢圓![]() 相交于
相交于![]() 兩點.
兩點.

(1)若直線![]() 恰好經過橢圓的左頂點,求弦長
恰好經過橢圓的左頂點,求弦長![]()
(2)設直線![]() 的斜率分別為
的斜率分別為![]() ,判斷
,判斷![]() 是否為定值,并說明理由
是否為定值,并說明理由
(3)求![]() ,面積的最小值.
,面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com