【題目】已知函數
，若存在
，使得
，則實數
的值為______．
【答案】
【解析】
函數f（x）可以看作是動點M（x，ex）與動點N（-a，-
）之間距離的平方，問題轉化為求直線上的動點到曲線的最小距離，由y=ex得，y′=ex=
，曲線上點M（-1，）到直線y=x的距離最小，要使f（x0）≤
，則f（x0）=，然后求解a即可．
函數f（x）=（x+a）2+（ex+）2，
函數f（x）可以看作是動點M（x，ex）與動點N（-a，-）之間距離的平方，
動點M在函數y=ex的圖象上，N在直線y=x的圖象上，
問題轉化為求直線上的動點到曲線的最小距離，
由y=ex得，y′=ex=，解得x=-1，
所以曲線上點M（-1，）到直線y=x的距離最小，最小距離d=
，
則f（x）≥，
根據題意，要使f（x0）≤，則f（x0）=，
此時N恰好為垂足，由KMN=-e，解得a= ．
故答案為：．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知雙曲線
的焦點是橢圓
： 
（
）的頂點，且橢圓與雙曲線的離心率互為倒數.
（Ⅰ）求橢圓
的方程；
（Ⅱ）設動點
， 
在橢圓
上，且
，記直線
在
軸上的截距為
，求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為更好地落實農民工工資保證金制度，南方某市勞動保障部門調查了
年下半年該市
名農民工（其中技術工、非技術工各
名）的月工資，得到這名農民工月工資的中位數為
百元（假設這名農民工的月工資均在
（百元）內）且月工資收入在
（百元）內的人數為
，并根據調查結果畫出如圖所示的頻率分布直方圖：
（Ⅰ）求
，
的值；
（Ⅱ）已知這名農民工中月工資高于平均數的技術工有
名，非技術工有
名，則能否在犯錯誤的概率不超過
的前提下認為是不是技術工與月工資是否高于平均數有關系？
參考公式及數據：
，其中
．
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
在直角坐標系
中，點P到兩點
，
的距離之和等于4，設點P的軌跡為
，直線
與C交于A，B兩點．
（Ⅰ）寫出C的方程；
（Ⅱ）若
，求k的值；
（Ⅲ）若點A在第一象限，證明：當k>0時，恒有||>||．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】1927年德國漢堡大學的學生考拉茲提出一個猜想：對于每一個正整數，如果它是奇數，就把它乘以3再加1，如果它是偶數，就把它除以2，這樣循環，最終結果都能得到1.如圖是為了驗證考拉茲猜想而設計的一個程序框圖，則①處應填寫的條件及輸出的結果i分別為（ ）
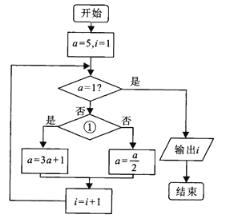
A.a是偶數？；5B.a是偶數？；6
C.a是奇數？；5D.a是奇數？；6
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用長為18 cm的鋼條圍成一個長方體形狀的框架，要求長方體的長與寬之比為2：1，問該長方體的長、寬、高各為多少時，其體積最大？最大體積是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知圓
及點
，
．
（1）若直線
平行于
，與圓
相交于
，
兩點，
，求直線
的方程；
（2）在圓
上是否存在點
，使得
？若存在，求點的個數；若不存在，說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
