
分析 (Ⅰ)根據導數的幾何意義即可求出k,b的值,
(Ⅱ)先求導,再分類討論,根據導數和函數的單調性關系即可求出.
(Ⅲ)當a=0時,若函數h(x)有兩個不同的零點,利用數形結合即可求b的取值范圍;
解答 解:(Ⅰ)∵函數f(x)=$\frac{1}{2}$ax2+lnx,x>0,
∴f′(x)=ax+$\frac{1}{x}$,
∵曲線y=f(x)與直線y=3x+b在x=1處相切,
∴f′(1)=a+1=3,
∴a=2,
∴f(1)=1+ln1=1,
∴1=3+b,
∴b=-2,
(Ⅱ)由(1)可得f′(x)=ax+$\frac{1}{x}$,
當a≥0時,f′(x)=ax+$\frac{1}{x}$>0恒成立,
∴f(x)在(0,+∞)上單調遞增,
當a<0時,令f′(x)=0,解得x=$\sqrt{\frac{1}{-a}}$=$\frac{\sqrt{-a}}{-a}$,
當x∈(0,$\frac{\sqrt{-a}}{-a}$)時,f′(x)>0,函數單調遞增,
當x∈($\frac{\sqrt{-a}}{-a}$,+∞)時,f′(x)<0,函數單調遞減,
(Ⅲ)a=0時,函數h(x)=f(x)+bx=lnx+bx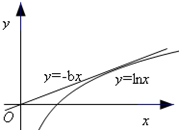
令m(x)=lnx,n(x)=-bx,
要使得h(x)有兩個零點,即使得m(x)和n(x)圖象有兩個交點(如圖),
容易求得m(x)和n(x)的切點為(e,1),
∴0<-b<$\frac{1}{e}$,即-$\frac{1}{e}$<b<0.
點評 本題主要考查函數單調性和導數之間的關系,考查考生的應用,運算量大,綜合性較強,屬于難題


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優(yōu)測試卷系列答案
全優(yōu)測試卷系列答案科目:高中數學 來源: 題型:解答題
 如圖,點M($\sqrt{3}$,$\sqrt{2}$)在橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且點M到兩焦點的距離之和為6.
如圖,點M($\sqrt{3}$,$\sqrt{2}$)在橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且點M到兩焦點的距離之和為6.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | g(x)是奇函數 | B. | g(x)的圖象關于直線x=-$\frac{π}{4}$對稱 | ||
| C. | g(x)在[$\frac{π}{4}$,$\frac{π}{2}$]上的增函數 | D. | 當x∈[$\frac{π}{6}$,$\frac{2π}{3}$]時,g(x)的值域是[-2,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
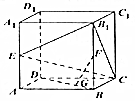 如圖,在長方體ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分別是AA1和BB1的中點,G是DB上的點,且DG=2GB.
如圖,在長方體ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分別是AA1和BB1的中點,G是DB上的點,且DG=2GB.查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com