【題目】關于圓周率
，數學發展史上出現過許多很有創意的求法，如著名的蒲豐實驗和查理斯實驗，受其啟發，我們也可以通過設計下面的實驗來估計的值：先請240名同學，每人隨機寫下兩個都小于1的正實數x，y組成的實數對
，再統計兩數能與1構成鈍角三角形三邊的數對的個數m；最后再根據計數m來估計π的值．假設統計結果是
，那么可以估計的近似值為____________．（用分數表示）
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，直線
過原點且傾斜角為
.以坐標原點
為極點，
軸正半軸為極軸建立坐標系，曲線
的極坐標方程為
.在平面直角坐標系中，曲線與曲線
關于直線
對稱.
（Ⅰ）求曲線的極坐標方程；
（Ⅱ）若直線
過原點且傾斜角為
，設直線與曲線相交于，
兩點，直線與曲線相交于，
兩點，當
變化時，求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國是全球最大的口罩生產國，在2020年3月份，我國每日口罩產量超一億只，已基本滿足國內人民的需求，但隨著疫情在全球范圍擴散，境外口罩需求量激增，世界衛生組織公開呼吁擴大口罩產能常見的口罩有
和
（分別阻擋不少于90.0%和95.0%的0.055到0.095微米的氯化鈉顆粒）兩種，某口罩廠兩條獨立的生產線分別生產和兩種口罩，為保證質量對其進行多項檢測并評分（滿分100分），規定總分大于或等于85分為合格，小于85分為次品，現從流水線上隨機抽取這兩種口罩各100個進行檢測并評分，結果如下：
總分 |
|
|
|
|
|
| 6 | 14 | 42 | 31 | 7 |
| 4 | 6 | 47 | 35 | 8 |
（1）試分別估計兩種口罩的合格率；
（2）假設生產一個口罩，若質量合格，則盈利3元，若為次品則虧損1元；生產一個口罩，若質量合格，則盈利8元，若為次品則虧損2元，在（1）的前提下，
①設
為生產一個口罩和生產一個口罩所得利潤的和，求隨機變量的分布列和數學期望；
②求生產4個口罩所得的利潤不少于8元的概率
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中心在原點的橢圓E的一個焦點與拋物線
的焦點關于直線
對稱，且橢圓E與坐標軸的一個交點坐標為
.
（1）求橢圓E的標準方程；
（2）過點
的直線l（直線的斜率k存在且不為0）交E于A，B兩點，交x軸于點P點A關于x軸的對稱點為D，直線BD交x軸于點Q.試探究
是否為定值？請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】工廠質檢員從生產線上每半個小時抽取一件產品并對其某個質量指標
進行檢測，一共抽取了
件產品，并得到如下統計表．該廠生產的產品在一年內所需的維護次數與指標有關，具體見下表.
質量指標 |
|
|
|
頻數 |
|
|
|
一年內所需維護次數 |
|
|
|
（1）以每個區間的中點值作為每組指標的代表，用上述樣本數據估計該廠產品的質量指標的平均值（保留兩位小數）；
（2）用分層抽樣的方法從上述樣本中先抽取
件產品，再從件產品中隨機抽取
件產品，求這件產品的指標都在
內的概率；
（3）已知該廠產品的維護費用為
元/次，工廠現推出一項服務：若消費者在購買該廠產品時每件多加
元，該產品即可一年內免費維護一次.將每件產品的購買支出和一年的維護支出之和稱為消費費用.假設這件產品每件都購買該服務，或者每件都不購買該服務，就這兩種情況分別計算每件產品的平均消費費用，并以此為決策依據，判斷消費者在購買每件產品時是否值得購買這項維護服務？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】疫情后，為了支持企業復工復產，某地政府決定向當地企業發放補助款，其中對納稅額在
萬元至
萬元（包括萬元和萬元）的小微企業做統一方案．方案要求同時具備下列兩個條件：①補助款
（萬元）隨企業原納稅額
（萬元）的增加而增加；②補助款不低于原納稅額（萬元）的
．經測算政府決定采用函數模型
（其中
為參數）作為補助款發放方案．
（1）判斷使用參數
是否滿足條件，并說明理由；
（2）求同時滿足條件①、②的參數的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，PD⊥平面ABCD，PD=DC=BC=2，AB//DC，AB=2CD，∠BCD=90°．
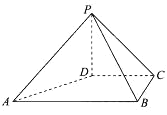
(1)求證：AD⊥PB；
(2)求點C到平面PAB的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某生物興趣小組對冬季晝夜溫差與反季節新品種大豆發芽數之間的關系進行研究，他們分別記錄了
月
日至11月25日每天的晝夜溫差與實驗室每天100顆種子的發芽數，得到以下表格
日期 | 11月21日 | 11月22日 | 11月23日 | 11月24日 | 11月25日 |
溫差( | 8 | 9 | 11 | 10 | 7 |
發芽數(顆) | 22 | 26 | 31 | 27 | 19 |
該興趣小組確定的研究方案是：先從這5組數據中選取2組數據，然后用剩下的3組數據求線性回歸方程，再用被選取的
組數據進行檢驗.
（1）求統計數據中發芽數的平均數與方差；
（2）若選取的是11月21日與11月25日的兩組數據，請根據11月22 日至11月24 日的數據，求出發芽數
關于溫差
的線性回歸方程
，若由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差不超過2，則認為得到的線性回歸方程是可靠的，問得到的線性回歸方程是否可靠？
附：線性回歸方程 中斜率和截距最小二乘估法計算公式：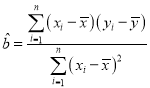
，
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
