
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 過原點且傾斜角為
過原點且傾斜角為![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立坐標系,曲線
軸正半軸為極軸建立坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .在平面直角坐標系
.在平面直角坐標系![]() 中,曲線
中,曲線![]() 與曲線
與曲線![]() 關于直線
關于直線![]() 對稱.
對稱.
(Ⅰ)求曲線![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)若直線![]() 過原點且傾斜角為
過原點且傾斜角為![]() ,設直線
,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,當
兩點,當![]() 變化時,求
變化時,求![]() 面積的最大值.
面積的最大值.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ)法一:將![]() 化為直角坐標方程,根據對稱關系用
化為直角坐標方程,根據對稱關系用![]() 上的點表示出
上的點表示出![]() 上點的坐標,代入
上點的坐標,代入![]() 方程得到
方程得到![]() 的直角坐標方程,再化為極坐標方程;法二:將
的直角坐標方程,再化為極坐標方程;法二:將![]() 化為極坐標方程,根據對稱關系將
化為極坐標方程,根據對稱關系將![]() 上的點用
上的點用![]() 上的點坐標表示出來,代入
上的點坐標表示出來,代入![]() 極坐標方程即可得到結果;(Ⅱ)利用
極坐標方程即可得到結果;(Ⅱ)利用![]() 和
和![]() 的極坐標方程與
的極坐標方程與![]() 的極坐標方程經
的極坐標方程經![]() 坐標用
坐標用![]() 表示,將所求面積表示為與
表示,將所求面積表示為與![]() 有關的三角函數解析式,通過三角函數值域求解方法求出所求最值.
有關的三角函數解析式,通過三角函數值域求解方法求出所求最值.
(Ⅰ)法一:由題可知,![]() 的直角坐標方程為:
的直角坐標方程為:![]() ,
,
設曲線![]() 上任意一點
上任意一點![]() 關于直線
關于直線![]() 對稱點為
對稱點為![]() ,
,
所以![]()
又因為![]() ,即
,即![]() ,
,
所以曲線![]() 的極坐標方程為:
的極坐標方程為:![]()
法二:由題可知,![]() 的極坐標方程為:
的極坐標方程為:![]()
![]() ,
,
設曲線![]() 上一點
上一點![]() 關于
關于![]()
![]() 的對稱點為
的對稱點為![]() ,
,
所以
又因為![]() ,即
,即![]() ,
,
所以曲線![]() 的極坐標方程為:
的極坐標方程為:![]()
(Ⅱ)直線![]() 的極坐標方程為:
的極坐標方程為:![]() ,直線
,直線![]() 的極坐標方程為:
的極坐標方程為:![]()
設![]() ,
,![]()
所以![]() 解得
解得![]() ,
,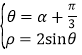 解得
解得![]()
![]()
![]()
因為:![]() ,所以
,所以![]()
當![]() 即
即![]() 時,
時,![]() ,
,![]() 取得最大值為:
取得最大值為:![]()


 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源: 題型:
【題目】在抽取彩票“雙色球”中獎號碼時,有33個紅色球,每個球的編號分別為01,02,…,33.一位彩民用隨機數表法選取6個號碼作為6個紅色球的編號,選取方法是從下面的隨機數表中第1行第6列的數字3開始,從左向右讀數,則依次選出的第3個紅色球的編號為( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.21B.32C.09D.20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接2022年北京冬季奧運會,普及冬奧知識,某校開展了“冰雪答題王”冬奧知識競賽活動.現從參加冬奧知識競賽活動的學生中隨機抽取了100名學生,將他們的比賽成績(滿分為100分)分為6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如圖所示的頻率分布直方圖.
,得到如圖所示的頻率分布直方圖.
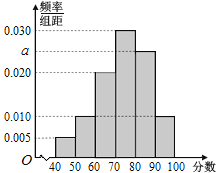
(1)求![]() 的值;
的值;
(2)估計這100名學生的平均成績(同一組中的數據用該組區間的中點值為代表);
(3)在抽取的100名學生中,規定:比賽成績不低于80分為“優秀”,比賽成績低于80分為“非優秀”.請將下面的2×2列聯表補充完整,并判斷是否有99.9%的把握認為“比賽成績是否優秀與性別有關”?
優秀 | 非優秀 | 合計 | |
男生 | 40 | ||
女生 | 50 | ||
合計 | 100 |
參考公式及數據:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年入冬以來,我市天氣反復.在下圖中統計了我市上個月前15天的氣溫,以及相對去年同期的氣溫差(今年氣溫-去年氣溫,單位:攝氏度),以下判斷錯誤的是( )
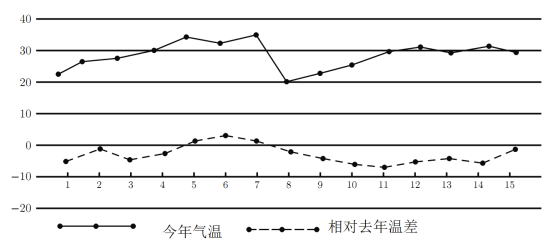
A.今年每天氣溫都比去年氣溫低B.今年的氣溫的平均值比去年低
C.今年8-12號氣溫持續上升D.今年8號氣溫最低
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
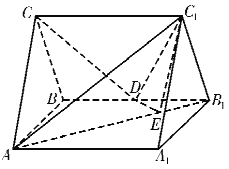
(I)若![]() 為
為![]() 上的一點,且
上的一點,且![]() 與直線
與直線![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的條件下,設異面直線![]() 與
與![]() 所成的角為45°,求點
所成的角為45°,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() ,直線
,直線![]() 過點
過點![]() ,且傾斜角為
,且傾斜角為![]() ,以
,以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,圓
軸的非負半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的參數方程和圓
的參數方程和圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的傾斜角的
的傾斜角的![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據統計,某地區植被覆蓋面積![]() 公頃
公頃![]() 與當地氣溫下降的度數
與當地氣溫下降的度數![]() 之間呈線性相關關系,對應數據如下:
之間呈線性相關關系,對應數據如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 請用最小二乘法求出y關于x的線性回歸方程;
請用最小二乘法求出y關于x的線性回歸方程;
![]() 根據
根據![]() 中所求線性回歸方程,如果植被覆蓋面積為300公頃,那么下降的氣溫大約是多少
中所求線性回歸方程,如果植被覆蓋面積為300公頃,那么下降的氣溫大約是多少![]() ?
?
參考公式:線性回歸方程![]() ;其中
;其中![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com