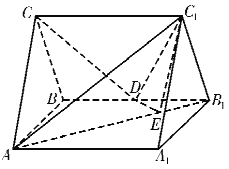
【題目】如圖，直三棱柱
中，
，
，
為
的中點.
（I）若
為
上的一點，且
與直線
垂直，求
的值；
（Ⅱ）在（I）的條件下，設異面直線與所成的角為45°，求點
到平面
的距離.
科目：高中數學 來源： 題型：
【題目】近年來，某地區積極踐行“綠水青山就是金山銀山”的綠色發展理念
年年初至
年年初，該地區綠化面積
（單位：平方公里）的數據如下表：
年份 |
|
|
|
|
|
|
|
年份代號 |
|
|
|
|
|
|
|
綠化面積 |
|
|
|
|
|
|
|
（1）求關于
的線性回歸方程；
（2）利用（1）中的回歸方程，預測該地區
年年初的綠化面積，并計算
年年初至年年初，該地區綠化面積的年平均增長率約為多少.
（附：回歸直線的斜率與截距的最小二乘法估計公式分別為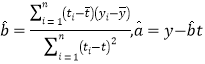
，
）
查看答案和解析>>
科目：高中數學 來源： 題型：
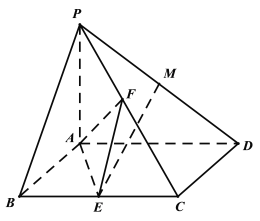
【題目】已知四棱錐
中，
平面
，底面為菱形，
，E是
中點，M是
的中點，F是
上的動點.
（1）求證：平面
平面
；
（2）直線
與平面所成角的正切值為
，當F是中點時，求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，直線
過原點且傾斜角為
.以坐標原點
為極點，
軸正半軸為極軸建立坐標系，曲線
的極坐標方程為
.在平面直角坐標系中，曲線與曲線
關于直線
對稱.
（Ⅰ）求曲線的極坐標方程；
（Ⅱ）若直線
過原點且傾斜角為
，設直線與曲線相交于，
兩點，直線與曲線相交于，
兩點，當
變化時，求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某車間有5名工人其中初級工2人，中級工2人，高級工1人
現從這5名工人中隨機抽取2名．
Ⅰ
求被抽取的2名工人都是初級工的概率；
Ⅱ求被抽取的2名工人中沒有中級工的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
：
，動點
，線段
與圓相交于點
，線段
的長度與點
到
軸的距離相等.
（1）求動點的軌跡
的方程；
（2）過點的直線
交曲線于
，
兩點，交圓于
，
兩點，其中在線段
上，在線段
上，求
的最小值及此時直線的斜率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區經過一年的新農村建設，農村的經濟收入增加了一倍．實現翻番．為更好地了解該地區農村的經濟收入變化情況，統計了該地區新農村建設前后農村的經濟收入構成比例．得到如下餅圖：
則下面結論中不正確的是
A. 新農村建設后，種植收入減少
B. 新農村建設后，其他收入增加了一倍以上
C. 新農村建設后，養殖收入增加了一倍
D. 新農村建設后，養殖收入與第三產業收入的總和超過了經濟收入的一半
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
