
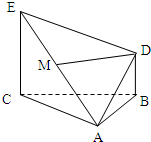
 如圖所示,△ABC為正三角形,EC⊥底面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點,
如圖所示,△ABC為正三角形,EC⊥底面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點,
| ||
. |
| ||
. |


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:高中數學 來源: 題型:
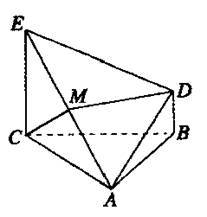
(08年聊城市三模)(12分) 如圖所示,△ABC為正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點.
(I)證明:DM∥平面ABC;
(II)證明:CM⊥DE;
(III)求平面ADE與平面ABC所成的二面角的大小(只考慮銳角情況).
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖所示,△ABC為直角三角形,∠C=90°,若![]() =(0,-4),M在
=(0,-4),M在![]() 軸上,且AM=
軸上,且AM=![]() ,點C在
,點C在![]() 軸上移動.
軸上移動.
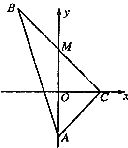
(Ⅰ)求點B的軌跡E的方程;
(Ⅱ)過點F(0,![]() )的直線
)的直線![]() 與曲線E交于P、Q兩點,設N(0,
與曲線E交于P、Q兩點,設N(0,![]() )(
)(![]() <0),
<0),![]() 與
與![]() 的夾角為
的夾角為![]() ,若
,若![]() ≤
≤![]() 等恒成立,求
等恒成立,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)設以點N為圓心,以![]() 半徑的圓與曲線E在第一象限的交點為H,若圓在點H處的切線與曲線E在點H處的切線互相垂直,求
半徑的圓與曲線E在第一象限的交點為H,若圓在點H處的切線與曲線E在點H處的切線互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:

求證:(1)DE=DA;
(2)平面MBD⊥平面ECA;
(3)平面DEA⊥平面ECA.
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖所示,△ABC為正三角形,CE⊥平面ABC,BD∥CE,且CE=AC=2BD,M是AE的中點.
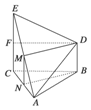
(1)求證:DE=DA;
(2)求證:平面BDM⊥平面ECA;
(3)求證:平面DEA⊥平面ECA.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com