
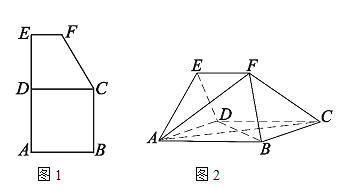
【題目】如圖1,平面五邊形![]() 是由邊長為2的正方形
是由邊長為2的正方形![]() 與上底為1,高為
與上底為1,高為![]() 直角梯形
直角梯形![]() 組合而成,將五邊形
組合而成,將五邊形![]() 沿著
沿著![]() 折疊,得到圖2所示的空間幾何體,其中
折疊,得到圖2所示的空間幾何體,其中![]() .
.
(1)證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)![]()
【解析】
(Ⅰ)以![]() 為原點,以平行于
為原點,以平行于![]() 的方向為
的方向為![]() 軸,平行于
軸,平行于![]() 的方向為
的方向為![]() 軸,建立空間直角坐標系.過
軸,建立空間直角坐標系.過![]() 點作
點作![]() 的高,交
的高,交![]() 于點
于點![]() ,先證明出
,先證明出![]() 平面
平面![]() ,設
,設![]() ,根據
,根據![]() ,可求出
,可求出![]() ,再利用向量法證明線線垂直,進而得到線面垂直;
,再利用向量法證明線線垂直,進而得到線面垂直;
(2)求出平面ABE的法向量![]() 、平面BCF的法向量
、平面BCF的法向量![]() ,由
,由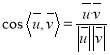 即可求出線面角.
即可求出線面角.
(1)以![]() 為原點,以平行于
為原點,以平行于![]() 的方向為
的方向為![]() 軸,平行于
軸,平行于![]() 的方向為
的方向為![]() 軸,建立如圖所示的空間直角坐標系.
軸,建立如圖所示的空間直角坐標系.
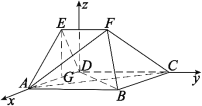
過![]() 點作
點作![]() 的高,交
的高,交![]() 于點
于點![]() .
.
由于![]() ,
,![]() ,
,![]()
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因為![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
設![]() ,由題設條件可得下列坐標:
,由題設條件可得下列坐標:
![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,由于
,由于![]() ,
,
所以![]() ,解得
,解得![]() ,
,
故![]() ,
,![]() .
.
可求![]() ,
,
且![]() ,
,![]() ,
,
從而![]() ,
,![]() .
.
因為![]() 平面
平面![]() ,且
,且![]() ,
,
故![]() 平面
平面![]() ;
;
(2)由(1)得![]() ,
,![]() ,
,![]() ,
,![]() .設平面
.設平面![]() 的法向量
的法向量![]() ,
,
由![]() 及
及![]() 得
得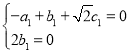
令![]() ,由此可得
,由此可得![]() .
.
設平面![]() 的法向量
的法向量![]() ,
,
由![]() 及
及![]() 得
得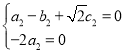
令![]() ,由此可得
,由此可得![]() .
.
則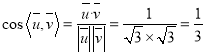 ,因為二面角
,因為二面角![]() 大于
大于![]() ,
,
則二面角![]() 的余弦值為
的余弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】近年來,南寧大力實施“二產補短板、三產強優勢、一產顯特色”策略,著力發展實體經濟,工業取得突飛猛進的發展.逐步形成了以電子信息、機械裝備、食品制糖、鋁深加工等為主的4大支柱產業.廣西洋浦南華糖業積極響應號召,大力研發新產品,為了對新研發的一批產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到一組銷售數據![]() ,如下表所示,已知
,如下表所示,已知![]() .
.

(1)求出q的值;
(2)已知變量x,y具有線性相關關系,求產品銷量y(件)關于試銷單價x(元)的線性回歸方程![]() ;
;
(3)用![]() 表示用(2)中所求的線性回歸方程得到的與
表示用(2)中所求的線性回歸方程得到的與![]() 對應的產品銷量的估計值.當銷售數據
對應的產品銷量的估計值.當銷售數據![]() 對應的殘差的絕對值
對應的殘差的絕對值![]() 時,則將銷售數據
時,則將銷售數據![]() 稱為一個“好數據”.現從6個銷售數據中任取3個,求“好數據”個數
稱為一個“好數據”.現從6個銷售數據中任取3個,求“好數據”個數![]() 的數學期望Eξ.
的數學期望Eξ.
(參考公式:線性回歸方程中![]() 的最小二乘估計分別為:
的最小二乘估計分別為: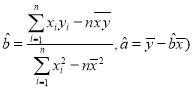
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面左圖是我省某地斜拉式大橋的圖片,合肥一中學數學興趣小組對大橋有關數據進行了測量,并將其簡化為右圖所示.其中橋塔AB,CD與橋面AC垂直,若![]() .
.

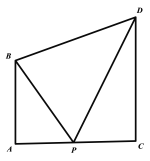
(1)當![]() 時,試確定點P在線段AC上的位置,并寫出求解過程;
時,試確定點P在線段AC上的位置,并寫出求解過程;
(2)要使得![]() 達到最大,試問點P在線段AC上何處?請寫出求解過程.
達到最大,試問點P在線段AC上何處?請寫出求解過程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() .已知函數
.已知函數![]() ,
,![]() .
.
(Ⅰ)求![]() 的單調區間;
的單調區間;
(Ⅱ)已知函數![]() 和
和![]() 的圖象在公共點(x0,y0)處有相同的切線,
的圖象在公共點(x0,y0)處有相同的切線,
(i)求證:![]() 在
在![]() 處的導數等于0;
處的導數等于0;
(ii)若關于x的不等式![]() 在區間
在區間![]() 上恒成立,求b的取值范圍.
上恒成立,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是曲線
是曲線![]() 上的動點,且點
上的動點,且點![]() 到
到![]() 的距離比它到x軸的距離大1.直線
的距離比它到x軸的距離大1.直線![]() 與直線
與直線![]() 的交點為
的交點為![]() .
.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)已知![]() 是曲線
是曲線![]() 上不同的兩點,線段
上不同的兩點,線段![]() 的垂直垂直平分線交曲線
的垂直垂直平分線交曲線![]() 于
于![]() 兩點,若
兩點,若![]() 的中點為
的中點為![]() ,則是否存在點
,則是否存在點![]() ,使得
,使得![]() 四點內接于以點
四點內接于以點![]() 為圓心的圓上;若存在,求出點
為圓心的圓上;若存在,求出點![]() 坐標以及圓
坐標以及圓![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是某公司2018年5~12月份研發費用(百萬元)和產品銷量(萬臺)的具體數據:
月 份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
研發費用(百萬元) | 2 | 3 | 6 | 10 | 21 | 13 | 15 | 18 |
產品銷量(萬臺) | 1 | 1 | 2 | 2.5 | 6 | 3.5 | 3.5 | 4.5 |
(Ⅰ)根據數據可知![]() 與
與![]() 之間存在線性相關關系,求出
之間存在線性相關關系,求出![]() 與
與![]() 的線性回歸方程(系數精確到0.01);
的線性回歸方程(系數精確到0.01);
(Ⅱ)該公司制定了如下獎勵制度:以![]() (單位:萬臺)表示日銷售,當
(單位:萬臺)表示日銷售,當![]()
![]() 時,每位員工每日獎勵200元;當
時,每位員工每日獎勵200元;當![]() 時,每位員工每日獎勵300元;當
時,每位員工每日獎勵300元;當![]() 時,每位員工每日獎勵400元.現已知該公司某月份日銷售
時,每位員工每日獎勵400元.現已知該公司某月份日銷售![]() (萬臺)服從正態分布
(萬臺)服從正態分布![]() (其中
(其中![]() 是2018年5-12月產品銷售平均數的二十分之一),請你估計每位員工該月(按30天計算)獲得獎勵金額總數大約多少元.
是2018年5-12月產品銷售平均數的二十分之一),請你估計每位員工該月(按30天計算)獲得獎勵金額總數大約多少元.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式:相關系數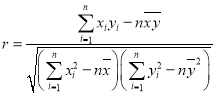 ,其回歸直線
,其回歸直線![]() 中的
中的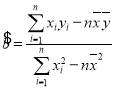 ,若隨機變量
,若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知定點
中,已知定點![]() ,點
,點![]() 在
在![]() 軸上運動,點
軸上運動,點![]() 在
在![]() 軸上運動,點
軸上運動,點![]() 為坐標平面內的動點,且滿足
為坐標平面內的動點,且滿足![]() ,
,![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過曲線![]() 第一象限上一點
第一象限上一點![]() (其中
(其中![]() )作切線交直線
)作切線交直線![]() 于點
于點![]() ,連結
,連結![]() 并延長交直線
并延長交直線![]() 于點
于點![]() ,求當
,求當![]() 面積取最小值時切點
面積取最小值時切點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com