
【題目】如圖,正三棱柱![]() 的底面邊長和側棱長都為2,
的底面邊長和側棱長都為2,![]() 是
是![]() 的中點.
的中點.
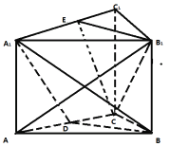
(1)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在指出點
,若存在指出點![]() 在線段
在線段![]() 上的位置,若不存在,請說明理由;
上的位置,若不存在,請說明理由;
(2)求直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)存在,點![]() 為線段
為線段![]() 的中點(2)
的中點(2)![]() .
.
【解析】
(1)設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,以
,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() 為
為![]() 、
、![]() 、
、![]() 軸建立空間直角坐標系,先求得平面
軸建立空間直角坐標系,先求得平面![]() 的法向量
的法向量![]() ,若平面
,若平面![]() 平面
平面![]() ,則
,則![]() 平面
平面![]() ,進而求解即可;
,進而求解即可;
(2)由(1),利用![]() 與
與![]() 求解即可
求解即可
(1)證明:存在點![]() 為線段
為線段![]() 的中點,使得平面
的中點,使得平面![]() 平面
平面![]() ,
,
設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
,
以![]() 為坐標原點,分別以
為坐標原點,分別以![]() 為
為![]() 、
、![]() 、
、![]() 軸建立空間直角坐標系,如圖所示,
軸建立空間直角坐標系,如圖所示,
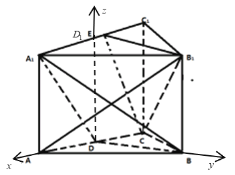
因為正三棱柱![]() 的底面邊長和側棱長都為2,
的底面邊長和側棱長都為2,![]() 是
是![]() 的中點,
的中點,
所以在![]() 中,
中,![]() ,
,
則![]() ,
,
所以![]() ,
,
設![]() 為平面
為平面![]() 的法向量,
的法向量,
則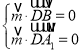 即
即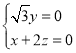 ,設
,設![]() ,則
,則![]() ,所以
,所以![]() ;
;
因為![]() ,
,
![]() ,所以
,所以![]() ,
,
若線段![]() 上存在點
上存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ,
,
設點![]() 坐標為
坐標為![]() ,則
,則![]() ,
,
因為平面![]() 平面
平面![]() ,所以
,所以![]() 也為平面
也為平面![]() 的法向量,即
的法向量,即![]() ,
,
則![]() ,所以
,所以![]() ,所以點
,所以點![]() 為線段
為線段![]() 的中點
的中點
(2)解:由(1)得![]() 為平面
為平面![]() 的法向量,
的法向量,![]() ,
,
則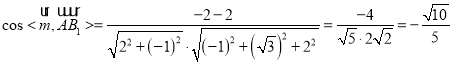 ,
,
所以直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 給出下列4個命題:①當且僅當
給出下列4個命題:①當且僅當![]() 時,
時,![]() 是偶函數;②函數
是偶函數;②函數![]() 一定存在零點;③函數在區間
一定存在零點;③函數在區間![]() 上單調遞減;④當
上單調遞減;④當![]() 時,函數
時,函數![]() 的最小值為
的最小值為![]() ,那么所有真命題的序號是_______.
,那么所有真命題的序號是_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“一帶一路”沿線的20國青年評選出了中國“新四大發明”:高鐵、支付寶、共享單車和網購.2019年春節期間,“支付寶大行動”用發紅包的方法刺激支付寶的使用.某商家統計前5名顧客掃描紅包所得金額分別為5.2元,2.9元,3.3元,5.9元,4.8元,商家從這5名顧客中隨機抽取3人贈送飲水杯.

(1)求獲得飲水杯的三人中至少有一人的紅包超過5元的概率;
(2)統計一周內每天使用支付寶付款的人數x與商家每天的凈利潤y元,得到7組數據,如表所示,并作出了散點圖.

(i)直接根據散點圖判斷,![]() 與
與![]() 出哪一個適合作為每天的凈利潤的回歸方程類型.
出哪一個適合作為每天的凈利潤的回歸方程類型.
(ii)根據(i)的判斷,建立y關于x的回歸方程;若商家當天的凈利潤至少是1400元,估計使用支付寶付款的人數至少是多少?(a,b,c,d的值取整數)
參考數據:
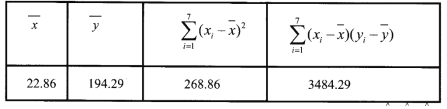
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為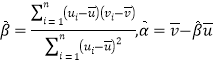 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() 和
和![]() ,動點P滿足
,動點P滿足![]() ,設動點P的軌跡為
,設動點P的軌跡為![]() ,以動點P到點
,以動點P到點![]() 距離的最大值為長軸,以點
距離的最大值為長軸,以點![]() 、
、![]() 為左、右焦點的橢圓為
為左、右焦點的橢圓為![]() ,則曲線
,則曲線![]() 和曲線
和曲線![]() 的交點到
的交點到![]() 軸的距離為_________.
軸的距離為_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知從1開始的連續奇數蛇形排列形成寶塔形數表,第一行為1,第二行為3,5,第三行為7,9,11,第四行為13,15,17,19,如圖所示,在寶塔形數表中位于第![]() 行,第
行,第![]() 列的數記為
列的數記為![]() ,比如
,比如![]() ,
,![]() ,
,![]() ,若
,若![]() ,則
,則![]() ( )
( )

A. 72B. 71C. 66D. 65
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國詩詞大會的播出引發了全民讀書熱,某學校語文老師在班里開展了一次詩詞默寫比賽,班里40名學生得分數據的莖葉圖如右圖,若規定得分不低于85分的學生得到“詩詞達人”的稱號,低于85分且不低于70分的學生得到“詩詞能手”的稱號,其他學生得到“詩詞愛好者”的稱號.根據該次比賽的成績按照稱號的不同進行分層抽樣抽選10名學生,則抽選的學生中獲得“詩詞能手”稱號的人數為( )

A. 6B. 5C. 4D. 2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P在曲線C:![]() 上,曲線C在點P處的切線為
上,曲線C在點P處的切線為![]() ,過點P且與直線
,過點P且與直線![]() 垂直的直線與曲線C的另一交點為Q,O為坐標原點,若OP⊥OQ,則點P的縱坐標為_______.
垂直的直線與曲線C的另一交點為Q,O為坐標原點,若OP⊥OQ,則點P的縱坐標為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面
的底面![]() 是邊長為1的正方形,
是邊長為1的正方形,![]() 底面
底面![]() ,且
,且![]() .
.

(1)若點![]() 、
、![]() 分別在棱
分別在棱![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,求證:
,求證:![]() 平面
平面![]() ;
;
(2)若點![]() 在線段
在線段![]() 上,且三棱錐
上,且三棱錐![]() 的體積為
的體積為![]() ,試求線段
,試求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com