Question

【題目】已知函數(shù).

（1）若，討論的單調(diào)性；

（2）若，且對于函數(shù)的圖象上兩點， ，存在，使得函數(shù)的圖象在處的切線.求證；.

Answer 1

【答案】(1)見解析(2)見證明

【解析】

(1)對函數(shù)求導(dǎo)，分別討論，以及，即可得出結(jié)果；

(2)根據(jù)題意，由導(dǎo)數(shù)幾何意義得到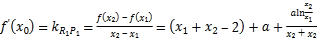，將證明轉(zhuǎn)化為證明即可，再令，設(shè) ，用導(dǎo)數(shù)方法判斷出的單調(diào)性，進而可得出結(jié)論成立.

（1）解：易得，函數(shù)的定義域為，

，

令，得或.

①當(dāng)時，時，，函數(shù)單調(diào)遞減；

時，，函數(shù)單調(diào)遞增.

此時，的減區(qū)間為，增區(qū)間為.

②當(dāng)時，時，，函數(shù)單調(diào)遞減；

或時，，函數(shù)單調(diào)遞增.

此時，的減區(qū)間為，增區(qū)間為，.

③當(dāng)時，時，，函數(shù)單調(diào)遞增；

此時，的減區(qū)間為.

綜上，當(dāng)時，的減區(qū)間為，增區(qū)間為：

當(dāng)時，的減區(qū)間為，增區(qū)間為.；

當(dāng)時，增區(qū)間為.

（2）證明：由題意及導(dǎo)數(shù)的幾何意義，得

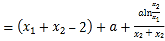
由（1）中得.

易知，導(dǎo)函數(shù) 在上為增函數(shù)，

所以，要證，只要證，

即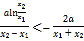，即證.

因為，不妨令，則 .

所以 ，

所以在上為增函數(shù)，

所以，即，

所以，即，

即.

故有（得證）.