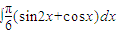
=
.
【答案】
分析:欲求積分,先求被積函數的原函數,由于(-

cos2x+sinx)′=sin2x+cosx,故原函數是-

cos2x+sinx,從而問題解決.
解答:解:

.
故填:

.
點評:本題主要考查了定積分的計算,屬于基礎題.
練習冊系列答案
相關習題
科目:高中數學
來源:2009年遼寧省丹東市高考數學二模試卷(理科)(解析版)
題型:選擇題
函數

是( )
A.最小正周期為π的偶函數
B.最小正周期為

的偶函數
C.最小正周期為π的奇函數
D.最小正周期為

的奇函數
查看答案和解析>>
科目:高中數學
來源:2006年安徽省高考數學試卷(理科)(解析版)
題型:解答題
已知函數f(x)在R上有定義,對任何實數a>0和任何實數x,都有f(ax)=af(x)
(Ⅰ)證明f(0)=0;
(Ⅱ)證明
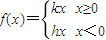
其中k和h均為常數;
(Ⅲ)當(Ⅱ)中的k>0時,設g(x)=
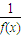
+f(x)(x>0),討論g(x)在(0,+∞)內的單調性并求極值.
查看答案和解析>>
科目:高中數學
來源:廣東省高考數學一輪復習:3.13 指數函數和對數函數(1)(解析版)
題型:選擇題
設a>1,若對于任意的x∈[a,2a],都有y∈[a,a2]滿足方程logax+logay=3,這時a的取值集合為( )
A.{a|1<a≤2}
B.{a|a≥2}
C.{a|2≤a≤3}
D.{2,3}
查看答案和解析>>
科目:高中數學
來源:2011年《龍門亮劍》高三數學(文科)一輪復習:第2章第8節(人教AB通用)(解析版)
題型:選擇題
某債券市場常年發行三種債券,A種面值為1 000元,一年到期本息和為1 040元;B種債券面值為1 000元,買入價為960元,一年到期本息之和為1 000元;C種面值為1 000元,半年到期本息和為1 020元.設三種債券的年收益率分別為a、b、c,則a、b、c的大小關系是( )
A.a=c<b
B.a<b<c
C.a<c<b
D.c<a<b
查看答案和解析>>
科目:高中數學
來源:2009年遼寧省丹東市高考數學二模試卷(理科)(解析版)
題型:解答題
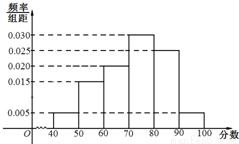
某校從參加高二年級學業水平測試的學生中抽出80名學生,其數學成績(均為整數)的頻率分布直方圖如圖所示.
(I)估計這次測試數學成績的平均分;
(II)假設在[90,100]段的學生的數學成績都不相同,且都超過94分.若將頻率視為概率,現用簡單隨機抽樣的方法,從95,96,97,98,99,100這6個數中任意抽取2個數,有放回地抽取了3次,記這3次抽取中,恰好是兩個學生的數學成績的次數為ξ,求ξ的分布列及數學期望Eξ.
查看答案和解析>>
科目:高中數學
來源:2009年遼寧省丹東市高考數學二模試卷(理科)(解析版)
題型:選擇題
已知點(x,y)滿足約束條件
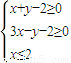
,若函數f(x)=log
a(x
2+1)(a>0且a≠1)圖象通過的定點是(m,n),則
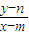
的最大值為( )
A.1
B.

C.2
D.4
查看答案和解析>>
科目:高中數學
來源:2004年安徽省高考數學試卷(理)(解析版)
題型:解答題
已知數列{an},滿足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),則{an}的通項 .
查看答案和解析>>
科目:高中數學
來源:2004年河南省高考數學試卷(理)(解析版)
題型:解答題
一接待中心有A、B、C、D四部熱線電話,已知某一時刻電話A、B占線的概率均為0.5,電話C、D占線的概率均為0.4,各部電話是否占線相互之間沒有影響.假設該時刻有ξ部電話占線.試求隨機變量ξ的概率分布和它的期望.
查看答案和解析>>

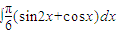 = .
= .  閱讀快車系列答案
閱讀快車系列答案 是( )
是( ) 的偶函數
的偶函數 的奇函數
的奇函數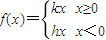 其中k和h均為常數;
其中k和h均為常數;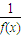 +f(x)(x>0),討論g(x)在(0,+∞)內的單調性并求極值.
+f(x)(x>0),討論g(x)在(0,+∞)內的單調性并求極值.
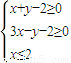 ,若函數f(x)=loga(x2+1)(a>0且a≠1)圖象通過的定點是(m,n),則
,若函數f(x)=loga(x2+1)(a>0且a≠1)圖象通過的定點是(m,n),則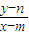 的最大值為( )
的最大值為( )