
【題目】已知冪函數f(x)=x![]() (m∈N*).
(m∈N*).
(1)試確定該函數的定義域,并指明該函數在其定義域上的單調性;
(2)若該函數還經過點(2, ![]() ),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
【答案】(1)詳見解析;(2)詳見解析.
【解析】試題分析:(1)先判斷冪函數的指數的奇偶,由m與m+1中必定有一個為偶數,可知m2+m為偶數,可得函數開偶次方,即函數定義域為[0,+∞),且在定義域內單調遞增;(2)由過點(2, ![]() )和m∈N*求出m的值,進而得出函數的定義域和單調性,列出不等式解出a的范圍即可.
)和m∈N*求出m的值,進而得出函數的定義域和單調性,列出不等式解出a的范圍即可.
試題解析:
(1)∵m2+m=m(m+1),m∈N*,
∴m與m+1中必定有一個為偶數,
∴m2+m為偶數,
∴函數f(x)=x![]() (m∈N*)的定義域為[0,+∞),并且該函數在其定義域上為增函數.
(m∈N*)的定義域為[0,+∞),并且該函數在其定義域上為增函數.
(2)∵函數f(x)經過點(2,![]() ),
),
∴![]() =2
=2![]() ,即2
,即2![]() =2
=2![]() ,
,
∴m2+m=2,即m2+m-2=0.
∴m=1或m=-2.
又∵m∈N*,∴m=1.
∵f(x)在[0,+∞)上是增函數,
∴由f(2-a)>f(a-1)得
 解得1≤a<
解得1≤a<![]() .
.
故m的值為1,滿足條件f(2-a)>f(a-1)的實數a的取值范圍為![]() .
.
點睛:本題考查冪函數的定義和性質,屬于中檔題. 第一問先判斷冪函數的指數的奇偶,由m與m+1中必定有一個為偶數,可知m2+m為偶數,可得函數開偶次方,即函數定義域為[0,+∞),且在定義域內單調遞增;第二問由過點(2, ![]() )和m∈N*求出m的值,進而得出函數的定義域和單調性, 寫出f(2-a)>f(a-1)的等價條件求解即可.
)和m∈N*求出m的值,進而得出函數的定義域和單調性, 寫出f(2-a)>f(a-1)的等價條件求解即可.


科目:高中數學 來源: 題型:
【題目】已知f(x)在R上是單調遞減的一次函數,且f(f(x))=4x-1.
(1)求f(x);
(2)求函數y=f(x)+x2-x在x∈[-1,2]上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1: ![]() (t為參數)曲線C2:
(t為參數)曲線C2:![]() +y2=4.
+y2=4.
(1)在同一平面直角坐標系中,將曲線C2上的點按坐標變換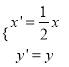 后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
(2)若C1上的點P對應的參數為t=π/2,Q為C′上的動點,求PQ中點M到直線C3: ![]() (t為參數)的距離的最小值
(t為參數)的距離的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() .若直線
.若直線![]() 與圓C相交于不同的兩點P,Q.
與圓C相交于不同的兩點P,Q.
(Ⅰ)寫出圓C的直角坐標方程,并求圓心的坐標與半徑;
(Ⅱ)若弦長|PQ|=4,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了制定合理的節電方案,供電局對居民用電情況進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:度),將數據按照![]() ,
,![]() 分成9組,制成了如圖所示的頻率直方圖.
分成9組,制成了如圖所示的頻率直方圖.
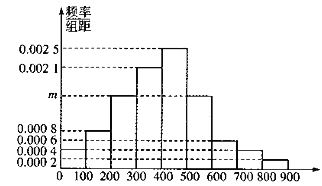
(1)求直方圖中![]() 的值并估計居民月均用電量的中位數;
的值并估計居民月均用電量的中位數;
(2)從樣本里月均用電量不低于700度的用戶中隨機抽取4戶,用![]() 表示月均用電量不低于800度的用戶數,求隨機變量
表示月均用電量不低于800度的用戶數,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(10分)設![]() 和
和![]() 分別是先后拋擲一枚骰子得到的點數,用隨機變量
分別是先后拋擲一枚骰子得到的點數,用隨機變量![]() 表示方程
表示方程
![]() 實根的個數(重根按一個計).
實根的個數(重根按一個計).
(Ⅰ)求方程![]() 有實根的概率;
有實根的概率;
(Ⅱ)求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)求在先后兩次出現的點數中有5的條件下,方程![]() 有實根的概率.
有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個正數a,b,可按規則![]() 擴充為一個新數c,在a,b,c三個數中取兩個較大的數,按上述規則擴充得到一個新數,依次下去,將每擴充一次得到一個新數稱為一次操作.
擴充為一個新數c,在a,b,c三個數中取兩個較大的數,按上述規則擴充得到一個新數,依次下去,將每擴充一次得到一個新數稱為一次操作.
(1)若a=1,b=3,按上述規則操作三次,擴充所得的數是_____________;
(2)若p>q>0,經過6次操作后擴充所得的數為![]() (m,n為正整數),
(m,n為正整數),
則m,n的值分別為____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com