【題目】已知冪函數f(x)＝x
(m∈N*)的圖象關于y軸對稱，且在(0，＋∞)上是減函數，求滿足(a＋1) 
<(3－2a) 
的a的取值范圍．
【答案】
.
【解析】試題分析: 冪函數f(x)＝x
在(0，＋∞)上單調遞減，可得m2－2m－3<0,且m∈N*,可得m的值為1或2,又圖象關于y軸對稱，即函數為偶函數,將m=1和m=2分別代入檢驗,可得m=1成立,即f(x)＝
;又函數在(－∞，0)，(0，＋∞)上均為減函數，按照a+1與3-2a在同一單調區間上和不在同一區間上分三種情況討論,解出不等式求出a的取值范圍.
試題解析:
∵冪函數f(x)＝x
在(0，＋∞)上單調遞減，∴m2－2m－3<0，解得－1<m<3.∵m∈N*，∴m＝1,2.
又函數的圖象關于y軸對稱，∴m2－2m－3是偶數，而22－2×2－3＝－3為奇數，12－2×1－3＝－4為偶數，
∴m＝1.
而f(x)＝x
在(－∞，0)，(0，＋∞)上均為減函數，∴(a＋1) 
<(3－2a) 
等價于a＋1>3－2a>0或0>a＋1>3－2a或a＋1<0<3－2a.解得a<－1或
<a<
.
故a的取值范圍為
.
科目：高中數學 來源： 題型：
【題目】試求下列函數的定義域與值域：
(1)f(x)＝(x－1)2＋1，x∈{－1,0,1,2,3}；
(2)f(x)＝(x－1)2＋1；
(3)f(x)＝
；
(4)f(x)＝x－
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數
滿足
（
），且
.
（1）求
的解析式；
（2）若關于
的方程
在區間
上有唯一實數根，求實數
的取值范圍（注：相等的實數根算一個）.
（3）函數
，試問是否存在實數
，使得對任意
， 
都有
成立，若存在，求出實數
的取值范圍，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知冪函數f(x)＝x
(m∈N*)．
(1)試確定該函數的定義域，并指明該函數在其定義域上的單調性；
(2)若該函數還經過點(2， 
)，試確定m的值，并求滿足條件f(2－a)＞f(a－1)的實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2015男籃亞錦賽決賽階段，中國男籃以9連勝的不敗戰績贏得第28屆亞錦賽冠軍，同時拿到亞洲唯一1張直通里約奧運會的入場券，賽后，中國男籃主力易建聯榮膺本屆亞錦賽
（最有價值球員），下表是易建聯在這9場比賽中投籃的統計數據．
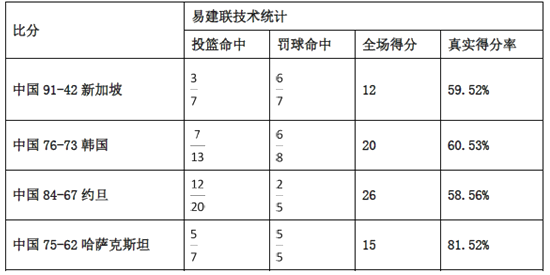
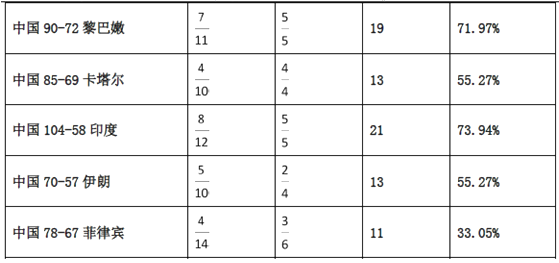
注：（1）表中
表示出手次命中
次；
（2）
（真實得分率）是衡量球員進攻的效率，其計算公式為：
（1）從上述9場比賽中隨機選擇一場，求易建聯在該場比賽中超過50%的概率；
（2）從上述9場比賽中隨機選擇一場，求易建聯在該場比賽中至少有一場超過60%的概率；
（3）用
來表示易建聯某場的得分，用
來表示中國隊該場的總分，畫出散點圖如圖所示，請根據散點圖判斷與之間是否具有線性相關關系？結合實際簡單說明理由．
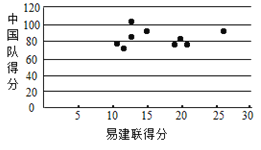
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l、m，平面α、β，下列命題正確的是 ( )
A. l∥β，lαα∥β
B. l∥β，m∥β，lα，mαα∥β
C. l∥m，lα，mβα∥β
D. l∥β，m∥β，lα，mα，l∩m＝Mα∥β
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
