
【題目】2020年新型冠狀病毒肺炎(簡稱“新冠肺炎”)成為威脅全球的公共衛生問題,中醫藥在本次新冠肺炎的治療中發揮了重要作用.研究人員對66例普通型新冠肺炎恢復期患者進行了中醫臨床特征分析,發現主要證型有氣陰兩虛證與肺脾氣虛證,同時可能兼夾濕證.為研究這兩種主要證型在兼夾濕證的難易上是否有差異,研究人員將濕證癥狀分級量化,將所有肺脾氣虛證患者的量化分作成莖葉圖.
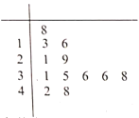
(1)若量化分不低于16分,即可診斷為兼夾濕證,請參考莖葉圖,完成下面![]() 列聯表.
列聯表.
夾濕證 | 非夾濕證 | 合計 | |
氣陰兩虛 | 20 | ||
肺脾氣虛 | |||
合計 | 66 |
(2)根據此資料,能否有99%的把握認為兩種主要證型在兼夾濕證的難易上有差異?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
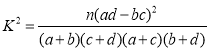
 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系內,點A,B的坐標分別為![]() ,
,![]() ,P是坐標平面內的動點,且直線
,P是坐標平面內的動點,且直線![]() ,
,![]() 的斜率之積等于
的斜率之積等于![]() .設點P的軌跡為C.
.設點P的軌跡為C.
(1)求軌跡C的方程;
(2)某同學對軌跡C的性質進行探究后發現:若過點![]() 且傾斜角不為0的直線
且傾斜角不為0的直線![]() 與軌跡C相交于M,N兩點,則直線
與軌跡C相交于M,N兩點,則直線![]() ,
,![]() 的交點Q在一條定直線上.此結論是否正確?若正確,請給予證明,并求出定直線方程;若不正確,請說明理由.
的交點Q在一條定直線上.此結論是否正確?若正確,請給予證明,并求出定直線方程;若不正確,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校數學建模小組為了研究雙層玻璃窗戶中每層玻璃厚度![]() (每層玻璃的厚度相同)及兩層玻璃間夾空氣層厚度
(每層玻璃的厚度相同)及兩層玻璃間夾空氣層厚度![]() 對保溫效果的影響,利用熱傳導定律得到熱傳導量
對保溫效果的影響,利用熱傳導定律得到熱傳導量![]() 滿足關系式
滿足關系式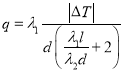 ,其中玻璃的熱傳導系數
,其中玻璃的熱傳導系數![]() 焦耳/(厘米·度),不流通、干燥空氣的熱傳導系數
焦耳/(厘米·度),不流通、干燥空氣的熱傳導系數![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 為室內外溫度差,
為室內外溫度差,![]() 值越小,保溫效果越好,現有4種型號的雙層玻璃窗戶,具體數據如下表:
值越小,保溫效果越好,現有4種型號的雙層玻璃窗戶,具體數據如下表:
型號 | 每層玻璃厚度 | 玻璃間夾空氣層厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
則保溫效果最好的雙層玻璃的型號是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型
查看答案和解析>>
科目:高中數學 來源: 題型:
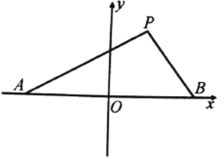
【題目】如圖,設點![]() 的坐標分別為
的坐標分別為![]() ,直線
,直線![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為
的軌跡為![]() ,點
,點![]() 是軌跡為
是軌跡為![]() 上不同于
上不同于![]() 的兩點,且滿足
的兩點,且滿足![]() ,求證:
,求證:![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D與AD1交于點E,AA1=AD=2AB=4.
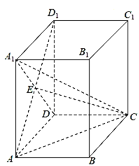
(1)證明:AE⊥平面ECD;
(2)求點C1到平面AEC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四面體![]() 中,棱
中,棱![]() ,
,![]() 所在直線所成角為
所在直線所成角為![]() ,且
,且![]() ,
,![]() ,
,![]() ,面
,面![]() 和面
和面![]() 所成的銳二面角為
所成的銳二面角為![]() ,面
,面![]() 和面
和面![]() 所成的銳二面角為
所成的銳二面角為![]() ,當四面體
,當四面體![]() 的體積取得最大值時( ).
的體積取得最大值時( ).
A.![]() B.
B.![]() C.
C.![]() D.不能確定
D.不能確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年4月8日,武漢市雷神山醫院為確診新型冠狀病毒肺炎患者,需要檢測核酸是否為陽性,現有![]() 份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測
份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測![]() 次;(2)混合檢測,將其中
次;(2)混合檢測,將其中![]() (
(![]() ,且
,且![]() )份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這
)份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這![]() 份核酸樣本全為陰性,因而這
份核酸樣本全為陰性,因而這![]() 份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這
份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這![]() 份核酸樣本究竟哪幾份為陽性,就要對這
份核酸樣本究竟哪幾份為陽性,就要對這![]() 份樣本再逐份檢測,此時這
份樣本再逐份檢測,此時這![]() 份核酸樣本的檢測次數總共為
份核酸樣本的檢測次數總共為![]() 次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為
次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為![]() .
.
(1)假設有5份核酸樣本,其中只有2份樣本為陽性,若采用逐份檢測方式,求恰好經過4次檢測就能把陽性樣本全部檢測出來的概率.
(2)現取其中![]() (
(![]() ,且
,且![]() )份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為
)份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為![]() ,采用混合檢測方式,樣本需要檢測的總次數為
,采用混合檢測方式,樣本需要檢測的總次數為![]() .
.
①試運用概率統計的知識,若![]() ,試求
,試求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ;
;
②若![]() ,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求
,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求![]() 的最大值.
的最大值.
參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 分別為
分別為![]() 內角
內角![]() 的對邊,若
的對邊,若![]() 是銳角三角形,需要同時滿足下列四個條件中的三個:
是銳角三角形,需要同時滿足下列四個條件中的三個:
①![]() ②
②![]() ③
③![]() ④
④![]()
(1)條件①④能否同時滿足,請說明理由;
(2)以上四個條件,請在滿足三角形有解的所有組合中任選一組,并求出對應的![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com