
【題目】2020年春節期間,新型冠狀病毒(2019﹣nCoV)疫情牽動每一個中國人的心,危難時刻全國人民眾志成城.共克時艱,為疫區助力.我國S省Q市共100家商家及個人為緩解湖北省抗疫消毒物資壓力,募捐價值百萬的物資對口輸送湖北省H市.
(1)現對100家商家抽取5家,其中2家來自A地,3家來自B地,從選中的這5家中,選出3家進行調研.求選出3家中1家來自A地,2家來自B地的概率.
(2)該市一商家考慮增加先進生產技術投入,該商家欲預測先進生產技術投入為49千元的月產增量.現用以往的先進技術投入xi(千元)與月產增量yi(千件)(i=1,2,3,…,8)的數據繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線![]() 的附近,且:
的附近,且:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,根據所給的統計量,求y關于x回歸方程,并預測先進生產技術投入為49千元時的月產增量.
,根據所給的統計量,求y關于x回歸方程,并預測先進生產技術投入為49千元時的月產增量.
附:對于一組數據(u1,v1)(u2,v2),其回歸直線v=α+βu的斜率和截距的最小二乘法估計分別為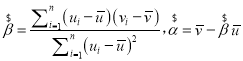
【答案】(1)0.6;(2)y=100.6+68![]() ,576.6千件.
,576.6千件.
【解析】
(1)設A地2家分為A1,A2,B地3家分為B1,B2,B3,由題意得,所有情況為10種,滿足條件的有6種,求出即可;
(2)由線性回歸方程公式,求出a,b,再求出線性回歸方程,取x=49代入求出即可.
(1)設A地2家分為A1,A2,B地3家分為B1,B2,B3,由題意得,所有情況為:
(A1,A2,B1),(A1,A2,B2),(A1,A2,B3),(A1,B1,B2),(A1,B1,B3),
(A1,B2,B3),(A2,B1,B2),(A2,B1,B3),(A2,B2,B3),(B1,B2,B3),
共10種,其中A地1家,B地2家的有6個,故所求的概率為![]() ;
;
(2)由線性回歸方程公式, ,
,
且a![]() ,
,
所以線性回歸方程為:y=100.6+68![]() ,
,
當x=49時,年銷售量y的預報值y=100.6+68×7=576.6千件,
故預測先進生產技術投入為49千元時的月產增量為576.6千件.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源: 題型:
【題目】甘肅省是土地荒漠化較為嚴重的省份,一代代治沙人為了固沙、治沙,改善生態環境,不斷地進行研究與實踐,實現了沙退人進.2019年,古浪縣八步沙林場“六老漢”三代人治沙群體作為優秀代表,被中宣部授予“時代楷模”稱號.在治沙過程中為檢測某種固沙方法的效果,治沙人在某一實驗沙丘的坡頂和坡腰各布設了50個風蝕插釬,以測量風蝕值(風蝕值是測量固沙效果的指標之一,數值越小表示該插釬處被風吹走的沙層厚度越小,說明固沙效果越好,數值為0表示該插針處沒有被風蝕)通過一段時間的觀測,治沙人記錄了坡頂和坡腰全部插釬測得的風蝕值(所測數據均不為整數),并繪制了相應的頻率分布直方圖.

(Ⅰ)根據直方圖估計“坡腰處一個插釬風蝕值小于30”的概率;
(Ⅱ)若一個插釬的風蝕值小于30,則該數據要標記“*”,否則不標記.根據以上直方圖,完成列聯表:
標記 | 不標記 | 合計 | |
坡腰 | |||
坡頂 | |||
合計 |
并判斷是否有![]() 的把握認為數據標記“*”與沙丘上插釬所布設的位置有關?
的把握認為數據標記“*”與沙丘上插釬所布設的位置有關?
(Ⅲ)坡頂和坡腰的平均風蝕值分別為![]() 和
和![]() ,若
,若![]() ,則可認為此固沙方法在坡頂和坡腰的固沙效果存在差異,試根據直方圖計算
,則可認為此固沙方法在坡頂和坡腰的固沙效果存在差異,試根據直方圖計算![]() 和
和![]() (同一組中的數據用該組區間的中點值為代表),并判斷該固沙方法在坡頂和坡腰的固沙效果是否存在差異.
(同一組中的數據用該組區間的中點值為代表),并判斷該固沙方法在坡頂和坡腰的固沙效果是否存在差異.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自湖北爆發新型冠狀病毒肺炎疫情以來,湖北某市醫護人員和醫療、生活物資嚴重匱乏,全國各地紛紛馳援.某運輸隊接到從武漢送往該市物資的任務,該運輸隊有8輛載重為6t的A型卡車,6輛載重為10t的B型卡車,10名駕駛員,要求此運輸隊每天至少運送240t物資.已知每輛卡車每天往返的次數為A型卡車5次,B型卡車4次,每輛卡車每天往返的成本A型卡車1200元,B型卡車1800元,則每天派出運輸隊所花的成本最低為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面![]() 平面ABC,P、P在平面ABC的同側,二面角
平面ABC,P、P在平面ABC的同側,二面角![]() 的平面角為鈍角,Q到平面ABC的距離為
的平面角為鈍角,Q到平面ABC的距離為![]() ,
,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() ,
,![]() ,
,![]() .
.
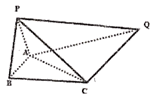
(1)求證:面![]() 平面PAB;
平面PAB;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的離心率為
)的離心率為![]() ,點
,點![]() 在橢圓C上,直線
在橢圓C上,直線![]() 與橢圓C交于不同的兩點A,B.
與橢圓C交于不同的兩點A,B.
(1)求橢圓C的方程;
(2)直線![]() ,
,![]() 分別交y軸于M,N兩點,問:x軸上是否存在點Q,使得
分別交y軸于M,N兩點,問:x軸上是否存在點Q,使得![]() ?若存在,求出點Q的坐標;若不存在,請說明理由.
?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com