
【題目】給出下列四個命題:
①命題“x∈R,cosx>0”的否定是“x0∈R,cosx0≤0”;
②若0<a<1,則函數(shù)f(x)=x2+ax-3只有一個零點;
③函數(shù)y=2![]() sinxcosx在
sinxcosx在![]() 上是單調(diào)遞減函數(shù);
上是單調(diào)遞減函數(shù);
④若lga+lgb=lg(a+b),則a+b的最小值為4.
其中真命題的序號是________.
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
: ![]() 的離心率
的離心率![]() ,左頂點為
,左頂點為![]() ,過點
,過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,交
,交![]() 軸于點
軸于點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 為
為![]() 的中點,是否存在定點
的中點,是否存在定點![]() ,對于任意的
,對于任意的![]() 都有
都有![]() ,若存在,求出點
,若存在,求出點![]() 的
的
坐標;若不存在說明理由;
(3)若過![]() 點作直線
點作直線![]() 的平行線交橢圓
的平行線交橢圓![]() 于點
于點![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系中,曲線![]() 的參數(shù)方程是
的參數(shù)方程是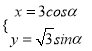 (
(![]() 為參數(shù))以原點為極點,
為參數(shù))以原點為極點, ![]() 軸正半軸為極軸,并取與直角坐標系相同的單位長度,建立極坐標系,曲線
軸正半軸為極軸,并取與直角坐標系相同的單位長度,建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求曲線![]() ,
, ![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 和
和![]() 上的任意點,求
上的任意點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)數(shù)列{an}的各項都為正數(shù),其前n項和為Sn,已知對任意n∈N*,Sn是![]() 和an的等差中項.
和an的等差中項.
(1)證明:數(shù)列{an}為等差數(shù)列;
(2)若bn=-n+5,求{an·bn}的最大項的值并求出取最大值時n的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某住宅小區(qū)為了使居民有一個優(yōu)雅舒適的生活環(huán)境,計劃建一個八邊形的休閑小區(qū),它的主體造型的平面圖是由兩個相同的矩形ABCD和EFGH構(gòu)成的面積為200平方米的十字型地域.現(xiàn)計劃在正方形MNPQ上建花壇,造價為4200元/平方米,在四個相同的矩形上(圖中陰影部分)鋪花崗巖地坪,造價為210元/平方米,再在四個空角上鋪草坪,造價為80元/平方米.

(1)設(shè)總造價為S元,AD的邊長為x米,DQ的邊長為y米,試建立S關(guān)于x的函數(shù)關(guān)系式;
(2)計劃至少要投入多少元,才能建造這個休閑小區(qū).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)等差數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,下列說法錯誤的是( )
,下列說法錯誤的是( )
A. 若![]() 有最大值,則
有最大值,則![]() 也有最大值
也有最大值
B. 若![]() 有最大值,則
有最大值,則![]() 也有最大值
也有最大值
C. 若數(shù)列![]() 不單調(diào),則數(shù)列
不單調(diào),則數(shù)列![]() 也不單調(diào)
也不單調(diào)
D. 若數(shù)列![]() 不單調(diào),則數(shù)列
不單調(diào),則數(shù)列![]() 也不單調(diào)
也不單調(diào)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知奇函數(shù)f(x)=(a-x)|x|,常數(shù)a∈R,且關(guān)于x的不等式mx2+m>f[f(x)]對所有的x∈[-2,2]恒成立,則實數(shù)m的取值范圍是______.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com