【題目】某住宅小區為了使居民有一個優雅舒適的生活環境，計劃建一個八邊形的休閑小區，它的主體造型的平面圖是由兩個相同的矩形ABCD和EFGH構成的面積為200平方米的十字型地域．現計劃在正方形MNPQ上建花壇，造價為4200元/平方米，在四個相同的矩形上（圖中陰影部分）鋪花崗巖地坪，造價為210元/平方米，再在四個空角上鋪草坪，造價為80元/平方米．
（1）設總造價為S元，AD的邊長為x米，DQ的邊長為y米，試建立S關于x的函數關系式；
（2）計劃至少要投入多少元，才能建造這個休閑小區．
【答案】（1）
；（2）118000元
【解析】
(1)根據由兩個相同的矩形ABCD和EFGH構成的十字形地域，四個小矩形加一個正方形面積共為200平方米得出AM的函數表達式，最后建立建立S與x的函數關系即得；
(2)利用基本不等式求出(1)中函數S的最小值，并求得當x取何值時，函數S的最小值即可．
(1)由題意，有AM=
，由AM＞0，有0＜x＜10
；
則S=4200x2+210(200-x2)+80×2×
；
S=4200x2+42000-210x2+
=4000x2+
+38000；
∴S關于x的函數關系式：
S=4000x2++38000，(0＜x＜10)；
(2)S=4000x2++38000≥2
+38000=118000；
當且僅當4000x2=時，即x=
時，∈(0，10)，S有最小值；
∴當x=米時，Smin=118000元．
故計劃至少要投入118000元，才能建造這個休閑小區．
靈星計算小達人系列答案
孟建平錯題本系列答案科目：高中數學 來源： 題型：
【題目】已知數列
的前n項和
．
若三角形的三邊長分別為
，
，
，求此三角形的面積；
探究數列中是否存在相鄰的三項，同時滿足以下兩個條件：
此三項可作為三角形三邊的長；
此三項構成的三角形最大角是最小角的2倍
若存在，找出這樣的三項，若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種商品在30天內每件的銷售價
（元）與時間
（天）的函數關系如圖表示，該商品在30天內日銷售量
（件）與時間（天）之間的關系為函數
.
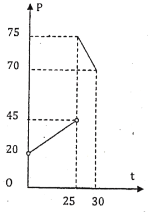
（1）根據提供的圖像，寫出商品每件的銷售價格與時間的函數關系式；
（2）若已知
，求該商品的日銷售金額的最大值，并指出日銷售金額最大的一天是30天中的第幾天。（日銷售金額=每件的銷售價格×日銷售量）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題：
①命題“x∈R，cosx>0”的否定是“x0∈R，cosx0≤0”；
②若0<a<1，則函數f(x)＝x2＋ax－3只有一個零點；
③函數y＝2
sinxcosx在
上是單調遞減函數；
④若lga＋lgb＝lg(a＋b)，則a＋b的最小值為4.
其中真命題的序號是________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過拋物線
的焦點作直線交拋物線于
，
兩點，若
，則
的值為（ ）
A. 10 B. 8 C. 6 D. 4
【答案】B
【解析】
根據過拋物線焦點的弦長公式，利用題目所給已知條件，求得弦長
.
根據過拋物線焦點的弦長公式有
.故選B.
【點睛】
本小題主要考查過拋物線焦點的弦長公式，即
.要注意只有過拋物線焦點的弦長才可以使用.屬于基礎題.
【題型】單選題
【結束】
10
【題目】已知橢圓
: 
的右頂點、上頂點分別為
、
，坐標原點到直線
的距離為
，且
，則橢圓的方程為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
