
【題目】如圖,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的邊長AB=3,側棱AA1=2,E是棱CC1的中點,點F滿足![]() =2
=2![]() .
.
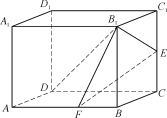
(1)求異面直線FE和DB1所成角的余弦值;
(2)記二面角E-B1F-A的大小為θ,求|cosθ|.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)先根據題意建立空間直角坐標系,求得向量![]() 和向量
和向量![]() 的坐標,再利用線線角的向量方法求解.
的坐標,再利用線線角的向量方法求解.
(2)先求得平面B1FE的一個法向量,易知平面AB1F的一個法向量,再利用面面角的向量方法求解.
(1) 在正四棱柱ABCDA1-B1C1D1中,
以![]() 為正交基底,建立如圖所示的空間直角坐標系D-xyz.
為正交基底,建立如圖所示的空間直角坐標系D-xyz.
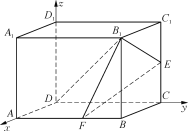
因為AB=3,AA1=2,
E是CC1的中點,![]() =2
=2![]() ,
,
所以E(0,3,1),F(3,2,0),B1(3,3,2).
從而![]() =(-3,1,1),
=(-3,1,1),![]() =(3,3,2).
=(3,3,2).
設異面直線FE和DB1所成的角為α,
則cosα=|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=![]() =
=![]() .
.
因此,異面直線FE和DB1所成角的余弦值為![]() .
.
(2)設平面B1FE的法向量為![]() =(x,y,).
=(x,y,).
因為![]() =(-3,1,1),
=(-3,1,1),![]() =(0,1,2),
=(0,1,2),
由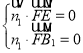 得
得![]() 所以
所以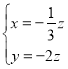
取z=-3,則平面B1FE的一個法向量為![]() =(1,6,-3).
=(1,6,-3).
又因為平面AB1F的一個法向量為![]() =(1,0,0),
=(1,0,0),
所以cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() .
.
因此cosθ|=| cos〈![]() ,
,![]() 〉|=
〉|=![]() .
.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案科目:高中數學 來源: 題型:
【題目】為了減輕家庭困難的高中學生的經濟負擔,讓更多的孩子接受良好的教育,國家施行高中生國家助學金政策,普通高中國家助學金平均資助標準為每生每年1500元,具體標準由各地結合實際在1000元至3000元范圍內確定,可以分為兩或三檔.各學校積極響應政府號召,通過各種形式宣傳國家助學金政策.為了解某高中學校對國家助學金政策的宣傳情況,擬采用隨機抽樣的方法抽取部分學生進行采訪調查.
(1)若該高中學校有2000名在校學生,編號分別為0001,0002,0003,…,2000,請用系統抽樣的方法,設計一個從這2000名學生中抽取50名學生的方案.(寫出必要的步驟)
(2)該校根據助學金政策將助學金分為3檔,1檔每年3000元,2檔每年2000元,3檔每年1000元,某班級共評定出3個1檔,2個2檔,1個3檔,若從該班獲得助學金的學生中選出2名寫感想,求這2名同學不在同一檔的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐![]() 的棱長均為6,其內有
的棱長均為6,其內有![]() 個小球,球
個小球,球![]() 與三棱錐
與三棱錐![]() 的四個面都相切,球
的四個面都相切,球![]() 與三棱錐
與三棱錐![]() 的三個面和球
的三個面和球![]() 都相切,如此類推,…,球
都相切,如此類推,…,球![]() 與三棱錐
與三棱錐![]() 的三個面和球
的三個面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),則球
),則球![]() 的體積等于__________,球
的體積等于__________,球![]() 的表面積等于__________.
的表面積等于__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平行六面體ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
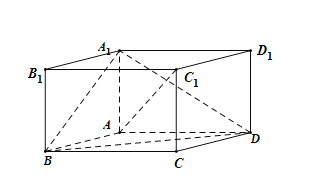
(1)求異面直線A1B與AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為3的正方體ABCDA1B1C1D1中,A1E=CF=1.
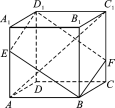
(1)求異面直線AC1與D1E所成角的余弦值;
(2)求直線AC1與平面BED1F所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M為PC的中點.
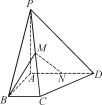
(1)求異面直線AP,BM所成角的余弦值;
(2)點N在線段AD上,且AN=λ,若直線MN與平面PBC所成角的正弦值為![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的兩焦點與短軸兩端點圍成面積為12的正方形.
)的兩焦點與短軸兩端點圍成面積為12的正方形.
(1)求橢圓C的標準方程;
(2)我們稱圓心在橢圓上運動,半徑為![]() 的圓是橢圓的“衛星圓”.過原點O作橢圓C的“衛星圓”的兩條切線,分別交橢圓C于A、B兩點,若直線
的圓是橢圓的“衛星圓”.過原點O作橢圓C的“衛星圓”的兩條切線,分別交橢圓C于A、B兩點,若直線![]() 、
、![]() 的斜率為
的斜率為![]() 、
、![]() ,當
,當![]() 時,求此時“衛星圓”的個數.
時,求此時“衛星圓”的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“雙11”促銷活動中,某商場為了吸引顧客,搞好促銷活動,采用“雙色球”定折扣的方式促銷,即:在紅、黃的兩個紙箱中分別裝有大小完全相同的紅、黃球各5個,每種顏色的5個球上標有1,2,3,4,5等5個數字,顧客結賬時,先分別從紅、黃的兩個紙箱中各取一球,按兩個球的數字之和為折扣打折,如![]() ,就按3折付款,并規定取球后不再增加商品.按此規定,顧客享有6折及以下折扣的概率是( )
,就按3折付款,并規定取球后不再增加商品.按此規定,顧客享有6折及以下折扣的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com