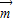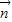、
是兩個單位向量，向量
=
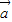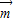-2
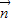，且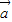
=（2，1），則
、
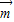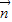的夾角為（ ）
閱讀快車系列答案科目：高中數學 來源：2012-2013學年廣東省深圳市寶安中學高一（上）期末數學試卷（解析版） 題型：解答題
=（2x-y+1，x+y-2），
=（2，-2），①當x、y為何值時，
與
共線？②是否存在實數x、y，使得
⊥
，且|
|=|
|？若存在，求出xy的值；若不存在，說明理由．
和
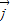是兩個單位向量，其夾角是90°，
，若
，求實數k的值．查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
=
=1+4-4
=5，求得 
=0，再根據兩個向量垂直的條件可得
、
的夾角等于90°．
、
是兩個單位向量，向量
=
-2
，且
=（2，1），
=
=1+4-4
=5，
=0，∴
，∴
、
的夾角為90°，
=0，是解題的關鍵． 
與
是兩個單位向量，其夾角為60°，且
，
的模；
與
是兩個單位向量，其夾角為60°，且
，
的模；
和
是兩個單位向量，其夾角是60°，求向量
與
的夾角θ．