
(本小題滿分14分)
已知函數 為常數,數列
為常數,數列 滿足:
滿足: ,
, ,
, .
.
(1)當 時,求數列
時,求數列 的通項公式;
的通項公式;
(2)在(1)的條件下,證明對 有:
有: ;
;
(3)若 ,且對
,且對 ,有
,有 ,證明:
,證明: .
.
(1) ,
,
(2)可以用裂項法求和進而證明也可以用數學歸納法證明
(3)可以用基本不等式證明也可以用導數證明,還可以利用數列的單調性證明
解析試題分析:(1)當 時,
時, ,
,
兩邊取倒數,得 , ……2分
, ……2分
故數列 是以
是以 為首項,為公差的等差數列,
為首項,為公差的等差數列,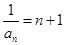 ,
, ,
, . ……4分
. ……4分
(2)證法1:由(1)知 ,故對
,故對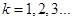

 ……6分
……6分
所以
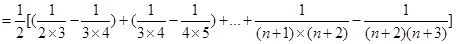

 . ……9分
. ……9分
[證法2:①當n=1時,等式左邊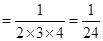 ,等式右邊
,等式右邊 ,左邊=右邊,等式成立; ……5分
,左邊=右邊,等式成立; ……5分
②假設當 時等式成立,
時等式成立,
即 ,
,
則當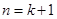 時
時


這就是說當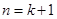 時,等式成立, ……8分
時,等式成立, ……8分
綜①②知對于 有:
有: . ……9分】
. ……9分】
(3)當 時,
時,
則 , ……10分
, ……10分
∵ ,
,
∴ ……11分
……11分


 . ……13分
. ……13分
∵ 與
與 不能同時成立,∴上式“=”不成立,
不能同時成立,∴上式“=”不成立,
即對 ,
, . ……14分
. ……14分
【證法二:當 時,
時, ,
,
則 ……10分
……10分
又



 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某同學在一次研究性學習中發現,以下五個式子的值都等于同一個常數:
①sin213°+cos217°-sin 13°cos 17°;
②sin215°+cos215°-sin 15°cos 15°;
③sin218°+cos212°-sin 18°cos 12°;
④sin2(-18°)+cos248°-sin(-18°)cos 48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos 55°.
(1)試從上述五個式子中選擇一個,求出這個常數;
(2)根據(1)的計算結果,將該同學的發現推廣為三角恒等式,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com