
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率
)的離心率![]() ,以上頂點和右焦點為直徑端點的圓與直線
,以上頂點和右焦點為直徑端點的圓與直線![]() 相切.
相切.
(1)求橢圓![]() 的標準方程.
的標準方程.
(2)是否存在斜率為2的直線,使得當直線與橢圓![]() 有兩個不同的交點
有兩個不同的交點![]() ,
,![]() 時,能在直線
時,能在直線![]() 上找到一點
上找到一點![]() ,在橢圓
,在橢圓![]() 上找到一點
上找到一點![]() ,滿足
,滿足![]() ?若存在,求出直線的方程;若不存在,請說明理由.
?若存在,求出直線的方程;若不存在,請說明理由.
【答案】(1)![]() .(2)橢圓
.(2)橢圓![]() 上不存在這樣的點
上不存在這樣的點![]() ,理由見解析
,理由見解析
【解析】
(1)利用離心率、上頂點和右焦點為直徑端點的圓與直線![]() 相切,列出方程組,求得
相切,列出方程組,求得![]() 的值,即可得到橢圓的方程;
的值,即可得到橢圓的方程;
(2)設設直線的方程為![]() ,設
,設![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的中點為
的中點為![]() ,聯(lián)立方程組,運用根與系數(shù)的關系及中點坐標公式,得到D為線段MN的中點,即D為線段PQ的中點,即可求解.
,聯(lián)立方程組,運用根與系數(shù)的關系及中點坐標公式,得到D為線段MN的中點,即D為線段PQ的中點,即可求解.
(1)由橢圓![]() :
:![]() (
(![]() )的離心率
)的離心率![]() ,得
,得![]() ,可得
,可得![]() .
.
上頂點為![]() ,右焦點為
,右焦點為![]() ,
,
可得以上頂點和右焦點為直徑端點的圓的方程為![]() 與直線
與直線![]() 相切,所以
相切,所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() ,∴橢圓的標準方程為
,∴橢圓的標準方程為![]() .
.
(2)橢圓![]() 上不存在這樣的點
上不存在這樣的點![]() ,理由如下:
,理由如下:
設直線的方程為![]() ,
,
設![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的中點為
的中點為![]() ,
,
由 消去
消去![]() ,得
,得![]() ,
,
所以![]() ,且
,且![]() ,故
,故![]() ,且
,且![]() ,
,
由![]() ,得
,得![]() ,
,
所以有![]() ,
,![]() .
.
(也可由![]() 知四邊形
知四邊形![]() 為平行四邊形,而
為平行四邊形,而![]() 為線段
為線段![]() 的中點,
的中點,
因此![]() 也為線段
也為線段![]() 的中點,所以
的中點,所以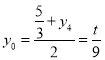 ,可得
,可得![]() )
)
又![]() ,所以
,所以![]() ,
,
與橢圓上點的縱坐標的取值范圍是![]() 矛盾,故橢圓
矛盾,故橢圓![]() 上不存在這樣的點
上不存在這樣的點![]() .
.


科目:高中數(shù)學 來源: 題型:
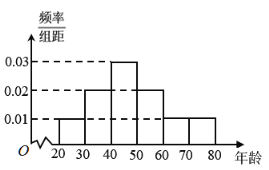
【題目】退休年齡延遲是平均預期壽命延長和人口老齡化背景下的一種趨勢.某機構為了了解某城市市民的年齡構成,從該城市市民中隨機抽取年齡段在[20,80]內的600人進行調查,并按年齡層次繪制頻率分布直方圖,如圖所示.若規(guī)定年齡分布在[60,80]內的人為“老年人”,將上述人口分布的頻率視為該城市年齡段在[20,80]的人口分布的概率.從該城市年齡段在[20,80]內的市民中隨機抽取3人,記抽到“老年人”的人數(shù)為![]() 則隨機變量
則隨機變量![]() 的數(shù)學期望為______.
的數(shù)學期望為______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為實常數(shù)).
為實常數(shù)).
(1)求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)若存在兩個不相等的正數(shù)![]() 、
、![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線y2=2px(p>0)上點M(3,m)到焦點F的距離為4.
(Ⅰ)求拋物線方程;
(Ⅱ)點P為準線上任意一點,AB為拋物線上過焦點的任意一條弦,設直線PA,PB,PF的斜率為k1,k2,k3,問是否存在實數(shù)λ,使得k1+k2=λk3恒成立.若存在,請求出λ的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市環(huán)保部門對該市市民進行了一次垃圾分類知識的網(wǎng)絡問卷調查,每位市民僅有一次參加機會,通過隨機抽樣,得到參與問卷調查的100人的得分(滿分:100分)數(shù)據(jù),統(tǒng)計結果如表所示:
組別 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若規(guī)定問卷得分不低于70分的市民稱為“環(huán)保關注者”,請完成答題卡中的![]() 列聯(lián)表,并判斷能否在犯錯誤概率不超過0.05的前提下,認為是否為“環(huán)保關注者”與性別有關?
列聯(lián)表,并判斷能否在犯錯誤概率不超過0.05的前提下,認為是否為“環(huán)保關注者”與性別有關?
(2)若問卷得分不低于80分的人稱為“環(huán)保達人”.視頻率為概率.
①在我市所有“環(huán)保達人”中,隨機抽取3人,求抽取的3人中,既有男“環(huán)保達人”又有女“環(huán)保達人”的概率;
②為了鼓勵市民關注環(huán)保,針對此次的調查制定了如下獎勵方案:“環(huán)保達人”獲得兩次抽獎活動;其他參與的市民獲得一次抽獎活動.每次抽獎獲得紅包的金額和對應的概率.如下表:
紅包金額(單位:元) | 10 | 20 |
概率 |
|
|
現(xiàn)某市民要參加此次問卷調查,記![]() (單位:元)為該市民參加間卷調查獲得的紅包金額,求
(單位:元)為該市民參加間卷調查獲得的紅包金額,求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的的參數(shù)方程為
的的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,點
軸的正半軸為極軸的極坐標系中,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 經(jīng)過點
經(jīng)過點![]() .曲線
.曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() 作直線
作直線![]() 的垂線交曲線
的垂線交曲線![]() 于
于![]() 兩點(
兩點(![]() 在
在![]() 軸上方),求
軸上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】一家商場銷售一種商品,該商品一天的需求量在![]() 范圍內等可能取值,該商品的進貨量也在
范圍內等可能取值,該商品的進貨量也在![]() 范圍內取值(每天進貨1次).這家商場每銷售一件該商品可獲利60元;若供不應求,可從其他商店調撥,銷售一件該商品可獲利40元;若供大于求,剩余的每處理一件該商品虧損20元.設該商品每天的需求量為
范圍內取值(每天進貨1次).這家商場每銷售一件該商品可獲利60元;若供不應求,可從其他商店調撥,銷售一件該商品可獲利40元;若供大于求,剩余的每處理一件該商品虧損20元.設該商品每天的需求量為![]() ,每天的進貨量為
,每天的進貨量為![]() 件,該商場銷售該商品的日利潤為
件,該商場銷售該商品的日利潤為![]() 元.
元.
(1)寫出這家商場銷售該商品的日利潤為![]() 關于需求量
關于需求量![]() 的函數(shù)表達式;
的函數(shù)表達式;
(2)寫出供大于求,銷售![]() 件商品時,日利潤
件商品時,日利潤![]() 的分布列;
的分布列;
(3)當進貨量![]() 多大時,該商場銷售該商品的日利潤的期望值最大?并求出日利潤的期望值的最大值.
多大時,該商場銷售該商品的日利潤的期望值最大?并求出日利潤的期望值的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() 為
為![]() 中點,沿直線
中點,沿直線![]() 將
將![]() 翻折成
翻折成![]() ,使平面
,使平面![]() 平面
平面![]() .點
.點![]() 分別在線段
分別在線段![]() 上,若沿直線
上,若沿直線![]() 將四邊形
將四邊形![]() 向上翻折,使
向上翻折,使![]() 與
與![]() 重合,則
重合,則![]() __________,四棱錐
__________,四棱錐![]() 的體積為__________.
的體積為__________.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com