
【題目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 這三個條件中任選一個,補充在下面問題中,若問題中的
這三個條件中任選一個,補充在下面問題中,若問題中的![]() 存在,求出
存在,求出![]() 和數列
和數列![]() 的通項公式與前
的通項公式與前![]() 項和;若
項和;若![]() 不存在,請說明理由.
不存在,請說明理由.
設![]() 為各項均為正數的數列
為各項均為正數的數列![]() 的前
的前![]() 項和,滿足________,是否存在
項和,滿足________,是否存在![]() ,使得數列
,使得數列![]() 成為等差數列?
成為等差數列?
【答案】答案不唯一,具體見解析
【解析】
由![]() ,用
,用![]() 換
換![]() 后得
后得![]() ,兩式相減得
,兩式相減得![]() ,若選擇①,由
,若選擇①,由![]() 可求得等差數列
可求得等差數列![]() 的通項公式及
的通項公式及![]() 值,前
值,前![]() 項和;若選擇②,由
項和;若選擇②,由![]() 得
得![]() 和
和![]() 的關系式,作為關于
的關系式,作為關于![]() 的二次方程,至少有正根,由根的分布得其條件是
的二次方程,至少有正根,由根的分布得其條件是![]() ,得出與已知矛盾的結論,說明不存在;若選擇③,由
,得出與已知矛盾的結論,說明不存在;若選擇③,由![]() ,同樣可求
,同樣可求![]() 和
和![]() .
.
解:選擇①,
因為![]() ,所以
,所以![]() ,兩式相減,得
,兩式相減,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
因為![]() ,且
,且![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,
,
把![]() 代入上式,得
代入上式,得![]() ,
,
當![]() 時,由
時,由![]() 及
及![]() ,得
,得![]() ,
,
所以![]() ,
,![]() ,滿足
,滿足![]() ,可知數列
,可知數列![]() 是以3為首項,以2為公差的等差數列.
是以3為首項,以2為公差的等差數列.
數列![]() 的通項公式為
的通項公式為![]() ,
,
數列![]() 的前
的前![]() 項和為
項和為![]() .
.
選擇②,
因為![]() ,所以
,所以![]() ,兩式相減,得
,兩式相減,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,
,
因為已知數列![]() 的各項均為正數,所以
的各項均為正數,所以![]() ,
,
因為關于![]() 的一元二次方程
的一元二次方程![]() 至少存在一個正實數解的充要條件是
至少存在一個正實數解的充要條件是
![]() ,
,
解得![]() ,
,
這與已知條件![]() 矛盾,所以滿足條件的
矛盾,所以滿足條件的![]() 不存在.
不存在.
(注:若![]() 存在兩個實數解分別為
存在兩個實數解分別為![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
當![]() 時,
時,![]() 的解一正一負;當
的解一正一負;當![]() 時,
時,![]() 的解一正一零;
的解一正一零;
當![]() 時,
時,![]() 的解均為正.
的解均為正.
所以方程![]() 至少存在一個正實數解,當且僅當
至少存在一個正實數解,當且僅當![]() .)
.)
選擇③,因為![]() ,所以
,所以![]() ,兩式相減,得
,兩式相減,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,又已知
,又已知![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,所以
,所以![]() ,
,
當![]() 時,由
時,由![]() 及
及![]() 得
得![]() ,
,
由![]() ,
,![]() 及
及![]() ,得
,得![]() ,
,
所以![]() 和
和![]() 滿足
滿足![]() ,
,
可知數列![]() 是以3為首項,以2為公差的等差數列,
是以3為首項,以2為公差的等差數列,
數列![]() 的通項公式為
的通項公式為![]() ,
,
數列![]() 的前
的前![]() 項和為
項和為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,過點
,過點![]() 且不過點
且不過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與直線
與直線![]() 交于點
交于點![]() .
.
(Ⅰ)若![]() 垂直于
垂直于![]() 軸,求直線
軸,求直線![]() 的斜率;
的斜率;
(Ⅱ)試判斷直線![]() 與直線
與直線![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市隨機選取![]() 位顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成如下統計表,其中“√”表示購買,“×”表示未購買.
位顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成如下統計表,其中“√”表示購買,“×”表示未購買.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估計顧客同時購買乙和丙的概率;
(Ⅱ)估計顧客在甲、乙、丙、丁中同時購買![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顧客購買了甲,則該顧客同時購買乙、丙、丁中那種商品的可能性最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
已知數列{an}和{bn}滿足:a1=λ,an+1=![]() 其中λ為實數,n為正整數.
其中λ為實數,n為正整數.
(Ⅰ)對任意實數λ,證明數列{an}不是等比數列;
(Ⅱ)試判斷數列{bn}是否為等比數列,并證明你的結論;
(Ⅲ)設0<a<b,Sn為數列{bn}的前n項和.是否存在實數λ,使得對任意正整數n,都有
a<Sn<b?若存在,求λ的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型科學競技真人秀節目挑選選手的方式為:不但要對選手的空間感知、照相式記憶能力進行考核,而且要讓選手經過名校最權威的腦力測試,120分以上才有機會入圍.某重點高校準備調查腦力測試成績是否與性別有關,在該高校隨機抽取男、女學生各100名,然后對這200名學生進行腦力測試.規定:分數不小于120分為“入圍學生”,分數小于120分為“未入圍學生”.已知男生入圍24人,女生未入圍80人.
(1)根據題意,填寫下面的2×2列聯表,并根據列聯表判斷是否有95%以上的把握認為腦力測試后是否為“入圍學生”與性別有關;
性別 | 入圍人數 | 未入圍人數 | 總計 |
男生 | |||
女生 | |||
總計 |
(2)用分層抽樣的方法從“入圍學生”中隨機抽取11名學生,求這11名學生中男、女生人數;若抽取的女生的腦力測試分數各不相同(每個人的分數都是整數),分別求這11名學生中女生測試分數平均分的最小值.
|
|
|
|
|
|
|
|
|
|
附: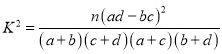 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 是拋物線
是拋物線![]() 上的兩個動點,
上的兩個動點,![]() 是坐標原點,向量
是坐標原點,向量![]() ,
,![]() 滿足
滿足![]() .設圓
.設圓![]() 的方程為
的方程為![]() .
.
(1)證明線段![]() 是圓
是圓![]() 的直徑;
的直徑;
(2)當圓![]() 的圓心到直線
的圓心到直線![]() 的距離的最小值為
的距離的最小值為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+2ax﹣lnx﹣1,a∈R.
(1)當a![]() 時,求f(x)的單調區間及極值;
時,求f(x)的單調區間及極值;
(2)若a為整數,且不等式f(x)≥x對任意x∈(0,+∞)恒成立,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:
有下述四個結論:
①![]() 是偶函數;②
是偶函數;②![]() 的最大值為
的最大值為![]() ;
;
③![]() 在
在![]() 有
有![]() 個零點;④
個零點;④![]() 在區間
在區間![]() 單調遞增.
單調遞增.
其中所有正確結論的編號是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com