
 如圖,已知放在同一平面上的兩個正三棱錐P-ABD、S-BCD(底面是正三角形且頂點在底面上的射影是底面正三角形的中心)的側(cè)棱長都相等.若AB=6,二面角P-BD-S的余弦值為
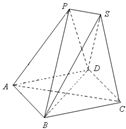
如圖,已知放在同一平面上的兩個正三棱錐P-ABD、S-BCD(底面是正三角形且頂點在底面上的射影是底面正三角形的中心)的側(cè)棱長都相等.若AB=6,二面角P-BD-S的余弦值為 .
. 分別作出兩個正三棱錐的高PN、SM,連接AC交BD于O,連接OP、OS
分別作出兩個正三棱錐的高PN、SM,連接AC交BD于O,連接OP、OS ,OM=
,OM=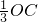 ∴MN=
∴MN=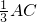
 AB=6
AB=6 ?MN=
?MN=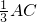 =2
=2

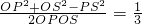


 ,AN=
,AN= ,
, =
=
 =
= ×
×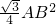 ×
× =
=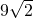
 =
=
 ,從而PS=2
,從而PS=2 ,在等腰三角形PSO中利用余弦定理結(jié)合二面角P-BD-S的余弦值為
,在等腰三角形PSO中利用余弦定理結(jié)合二面角P-BD-S的余弦值為 計算出PO長,再在Rt三角形POB中求出PB長,得到△PBD、△PBA都是等腰直角三角形,從而結(jié)合線面垂直的判定得到PB⊥平面PAD;
計算出PO長,再在Rt三角形POB中求出PB長,得到△PBD、△PBA都是等腰直角三角形,從而結(jié)合線面垂直的判定得到PB⊥平面PAD; ,從而得到正三棱錐P-ABD的體積為
,從而得到正三棱錐P-ABD的體積為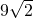 ,最終可得多面體SPABC的體積.
,最終可得多面體SPABC的體積.

科目:高中數(shù)學(xué) 來源: 題型:解答題
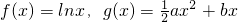 .
.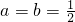 時,求函數(shù)h(x)=f(x)-g(x)的單調(diào)區(qū)間;
時,求函數(shù)h(x)=f(x)-g(x)的單調(diào)區(qū)間;查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
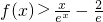 成立.
成立.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
 成立,那么一定有
成立,那么一定有查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 是否屬于M,并說明理由;
是否屬于M,并說明理由;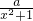 屬于M,求實數(shù)a的取值范圍.
屬于M,求實數(shù)a的取值范圍.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com