
【題目】如圖,四棱錐![]() 中,
中,![]() 為
為![]() 的中點.
的中點.

求證:![]() 平面
平面![]() .
.
【答案】證明見解析
【解析】
試題分析:方法一,取PA的中點H,連接EH、DH。證明四邊形DCEH是平行四邊形,可得CE∥DH,根據線面平行的判定定理可得![]() 平面
平面![]() .
.
方法二:取AB的中點F,連接CF、EF,證明平面CEF∥平面PAD,可得![]() 平面
平面![]() .
.
試題解析:
方法一: 如圖所示,取PA的中點H,連EH、DH.
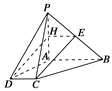
因為E為PB的中點,
所以EH∥AB,![]() 。
。
又AB∥CD,![]() ,
,
所以EH∥CD,EH=CD.
因此四邊形DCEH是平行四邊形,
所以CE∥DH.
又DH平面PAD,CE![]() 平面PAD,
平面PAD,
因此CE∥平面PAD.
方法二:如圖所示,取AB的中點F,連CF、EF,
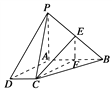
所以![]() ,又
,又![]() ,
,
所以AF=CD。
又AF∥CD,
所以四邊形AFCD為平行四邊形,
因此CF∥AD。
又CF![]() 平面PAD,AD平面PAD。
平面PAD,AD平面PAD。
所以CF∥平面PAD。
因為E,F分別為PB,AB的中點,
所以EF∥PA。
又EF![]() 平面PAD,PA平面PAD,
平面PAD,PA平面PAD,
所以EF∥平面PAD。
因為CF ∩ EF=F,
所以平面CEF∥平面PAD。
又CE平面CEF,
所以CE∥平面PAD。


 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|+|x+a|.
(Ⅰ)當a=2時,解不等式f(x)>6;
(Ⅱ)若關于x的不等式f(x)<a2﹣1有解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某店銷售進價為2元/件的產品![]() ,該店產品
,該店產品![]() 每日的銷售量
每日的銷售量![]() (單位:千件)與銷售價格
(單位:千件)與銷售價格![]() (單位:元/件)滿足關系式
(單位:元/件)滿足關系式![]() ,其中
,其中![]() .
.
(1)若產品![]() 銷售價格為4元/件,求該店每日銷售產品
銷售價格為4元/件,求該店每日銷售產品![]() 所獲得的利潤;
所獲得的利潤;
(2)試確定產品![]() 的銷售價格,使該店每日銷售產品
的銷售價格,使該店每日銷售產品![]() 所獲得的利潤最大.(保留1位小數)
所獲得的利潤最大.(保留1位小數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓錐的軸截面SAB是邊長為2的等邊三角形,O為底面中心,M為SO的中點,動點P在圓錐底面內(包括圓周).若AM⊥MP,則P點形成的軌跡的長度為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解甲、乙兩名同學的數學學習情況,對他們的![]() 次數學測試成績(滿分
次數學測試成績(滿分![]() 分)進行統計,作出如下的莖葉圖,其中
分)進行統計,作出如下的莖葉圖,其中![]() 處的數字模糊不清,已知甲同學成績的中位數是
處的數字模糊不清,已知甲同學成績的中位數是![]() ,乙同學成績的平均分是
,乙同學成績的平均分是![]() 分.
分.

(1)求![]() 和
和![]() 的值;
的值;
(2)現從成績在![]() 之間的試卷中隨機抽取兩份進行分析,求恰抽到一份甲同學試卷的概率.
之間的試卷中隨機抽取兩份進行分析,求恰抽到一份甲同學試卷的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線C1:ρsin2θ=4cosθ.以極點為坐標原點,極軸為x軸正半軸建立直角坐標系xOy,曲線C2的參數方程為: ![]() ,(θ∈[﹣
,(θ∈[﹣ ![]() ,
, ![]() ]),曲線C:
]),曲線C:  (t為參數).
(t為參數).
(Ⅰ)求C1的直角坐標方程;
(Ⅱ)C與C1相交于A,B,與C2相切于點Q,求|AQ|﹣|BQ|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com