
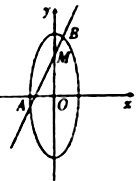
【題目】如圖,已知焦點在![]() 軸上的橢圓
軸上的橢圓![]() 的中心是原點
的中心是原點![]() ,離心率為
,離心率為![]() ,以橢圓
,以橢圓![]() 的端州的兩端點和兩焦點所圍成的四邊形的周長為8,直線
的端州的兩端點和兩焦點所圍成的四邊形的周長為8,直線![]() :
:![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于不同兩點
交于不同兩點![]() ,
,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】如圖,太湖一個角形湖灣![]() ( 常數
( 常數![]() 為銳角). 擬用長度為
為銳角). 擬用長度為![]() (
(![]() 為常數)的圍網圍成一個養殖區,有以下兩種方案可供選擇:
為常數)的圍網圍成一個養殖區,有以下兩種方案可供選擇:
方案一 如圖1,圍成扇形養殖區![]() ,其中
,其中![]() ;
;
方案二 如圖2,圍成三角形養殖區![]() ,其中
,其中![]() ;
;
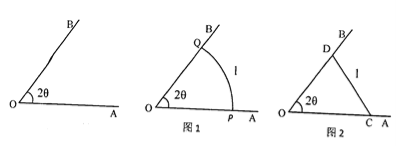
(1)求方案一中養殖區的面積![]() ;
;
(2)求方案二中養殖區的最大面積![]() ;
;
(3)為使養殖區的面積最大,應選擇何種方案?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若函數![]() 在
在![]() 處取得極值,求實數
處取得極值,求實數![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,函數![]() (其中
(其中![]() 為函數
為函數![]() 的導數)的圖像關于直線
的導數)的圖像關于直線![]() 對稱,求函數
對稱,求函數![]() 單調區間;
單調區間;
(Ⅲ)在(Ⅱ)的條件下,若對任意的![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 滿足
滿足![]() (
(![]() ;
; ![]() ,
, ![]() ),稱數列
),稱數列![]() 為
為![]() 數列,記
數列,記![]() 為其前
為其前![]() 項和.
項和.
(Ⅰ)寫出一個滿足![]() ,且
,且![]() 的
的![]() 數列
數列![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,證明:若
,證明:若![]() 數列
數列![]() 是遞增數列,則
是遞增數列,則![]() ;反之,若
;反之,若![]() ,則
,則![]() 數列
數列![]() 是遞增數列;
是遞增數列;
(Ⅲ)對任意給定的整數![]() (
(![]() ),是否存在首項為0的
),是否存在首項為0的![]() 數列
數列![]() ,使得
,使得![]() ?如果存在,寫出一個滿足條件的
?如果存在,寫出一個滿足條件的![]() 數列
數列![]() ;如果不存在,說明理由.
;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)求![]() 的展開式中
的展開式中![]() 的系數及展開式中各項系數之和;
的系數及展開式中各項系數之和;
(2)從0,2,3,4,5,6這6個數字中任取4個組成一個無重復數字的四位數,求滿足條件的四位數的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】劉徽是我國魏晉時期著名的數學家,他編著的《海島算經》中有一問題:“今有望海島,立兩表齊,高三丈,前后相去千步,令后表與前表相直。從前表卻行一百二十三步,人目著地取望島峰,與表末參合。從后表卻行百二十七步,人目著地取望島峰,亦與表末參合。問島高幾何?” 意思是:為了測量海島高度,立了兩根表,高均為5步,前后相距1000步,令后表與前表在同一直線上,從前表退行123步,人恰觀測到島峰,從后表退行127步,也恰觀測到島峰,則島峰的高度為( )(注:3丈=5步,1里=300步)
A. 4里55步 B. 3里125步 C. 7里125步 D. 6里55步
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列正確命題有__________.
①“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
②如果命題“![]() ”為假命題,則
”為假命題,則![]() 中至多有一個為真命題
中至多有一個為真命題
③設![]() ,若
,若![]() ,則
,則![]() 的最小值為
的最小值為![]()
④函數![]() 在
在![]() 上存在
上存在![]() ,使
,使![]() ,則a的取值范圍
,則a的取值范圍![]() 或
或![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究某種微生物的生長規律,需要了解環境溫度![]() (
(![]() )對該微生物的活性指標
)對該微生物的活性指標![]() 的影響,某實驗小組設計了一組實驗,并得到如表的實驗數據:
的影響,某實驗小組設計了一組實驗,并得到如表的實驗數據:
環境溫度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指標 |
|
|
|
|
|
|
|
(Ⅰ)由表中數據判斷![]() 關于
關于![]() 的關系較符合
的關系較符合![]() 還是
還是![]() ,并求
,并求![]() 關于
關于![]() 的回歸方程(
的回歸方程(![]() ,
,![]() 取整數);
取整數);
(Ⅱ)根據(Ⅰ)中的結果分析:若要求該種微生物的活性指標不能低于![]() ,則環境溫度應不得高于多少
,則環境溫度應不得高于多少![]() ?
?
附: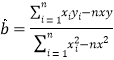 ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com