
 平面
平面 ,
,
 ,且
,且 ,(1)求證:BE//平面PDA;
,(1)求證:BE//平面PDA; 的中點,求證:
的中點,求證: 平面
平面 ;
; ,求平面PBE與平面ABCD所成的二面角的大小.
,求平面PBE與平面ABCD所成的二面角的大小. ,
,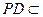 平面
平面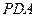 ,
,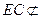 平面
平面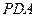
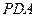 ,同理可得BC//平面
,同理可得BC//平面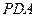 ---------------2分
---------------2分 平面EBC,BC
平面EBC,BC 平面EBC且
平面EBC且
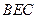 //平面
//平面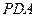 ----------3分又∵BE
----------3分又∵BE 平面EBC ∴BE//平面PDA---------4分
平面EBC ∴BE//平面PDA---------4分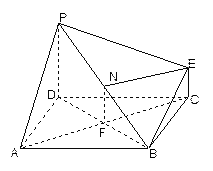 ∴
∴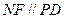 且
且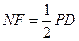 ,-------------6分
,-------------6分 且
且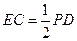
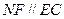 且
且
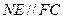

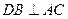 ,
, 平面
平面 ,
,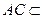 面
面 ∴
∴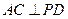 ,
,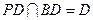 ∴
∴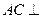 面
面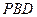 ∴
∴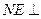 面
面 --------------9分
--------------9分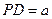
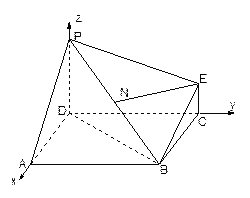 則
則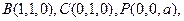
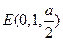 ,
,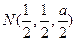 --------------------------------6分
--------------------------------6分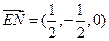 ,
,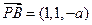 ,
,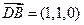
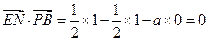 ,
,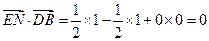
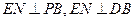 -------------8分∵
-------------8分∵ 、
、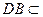 面
面 ,且
,且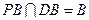
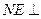 面
面 ------9分
------9分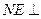 面
面 ∴
∴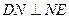 , ∵
, ∵ ,
,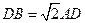
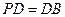 ∴
∴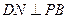 ∴
∴ 為平面PBE的法向量,設
為平面PBE的法向量,設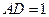 ,則
,則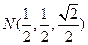
 =
=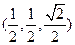 ---11分∵
---11分∵ 為平面ABCD的法向量,
為平面ABCD的法向量,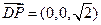 , --------12分
, --------12分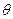 ,則
,則 -----------13分
-----------13分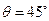 即平面PBE與平面ABCD所成的二面角為45°---------------------------------14分
即平面PBE與平面ABCD所成的二面角為45°---------------------------------14分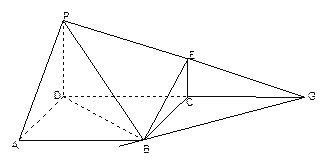 則GB為平面PBE與ABCD的交線-------10分
則GB為平面PBE與ABCD的交線-------10分 ∴
∴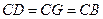
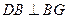 -------------------11分
-------------------11分 平面
平面 ,
,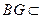 面
面
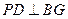 且
且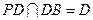
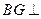 面
面 ∵
∵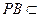 面
面
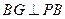 ∴
∴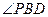 為平面PBE與
為平面PBE與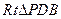 中∵
中∵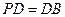 ∴
∴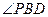 =45°即平面PBE與平面ABCD所成的二面角為45°-14分
=45°即平面PBE與平面ABCD所成的二面角為45°-14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
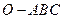 的三條側棱
的三條側棱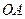 、
、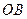 、
、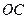 兩兩垂直,且長度均為2.
兩兩垂直,且長度均為2.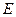 、
、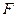 分別是
分別是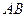 、
、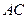 的中點,
的中點,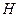 是
是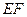 的中點,過
的中點,過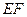 作平面與側棱
作平面與側棱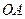 、
、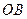 、
、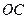 或其延長線分別相交于
或其延長線分別相交于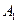 、
、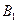 、
、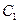 ,已知
,已知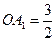 。
。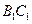 ⊥平面
⊥平面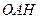 ;
;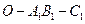 的大小。
的大小。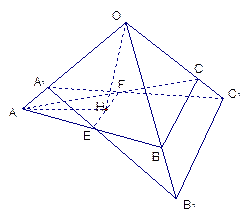
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 所在平面與圓
所在平面與圓 所在平面相交于
所在平面相交于 ,線段
,線段 為圓
為圓 的弦,
的弦,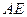 垂直于圓
垂直于圓 所在平面,垂足
所在平面,垂足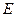 是圓
是圓 上異于
上異于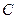 、
、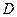 的點,
的點,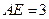 ,圓
,圓 的直徑為9.
的直徑為9.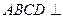 平面
平面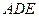 ;
;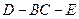 的平面角的正切值.
的平面角的正切值.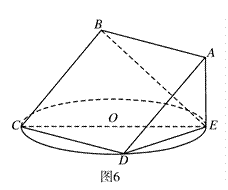
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 (如圖)底面是邊長為2的正方形.側棱
(如圖)底面是邊長為2的正方形.側棱 底面
底面 ,
,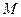 、
、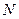 分別為
分別為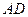 、
、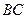 的中點,
的中點,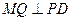 于
于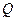 。
。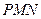 ⊥平面
⊥平面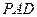 ;
;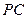 與平面
與平面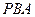 所成角的正弦值為
所成角的正弦值為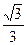 ,求PA的長;
,求PA的長;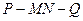 的余弦值。
的余弦值。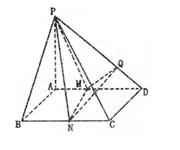
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.0個 | B.1個 | C.2個 | D.3個 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 系是( )
系是( )A.PO//平面 ABCD ABCD | B.PO 平面ABCD 平面ABCD |
| C.PO與平面ABCD斜交 | D.PO⊥平面ABCD |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com