
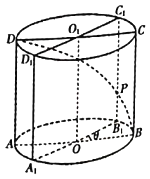
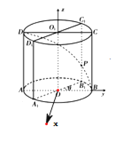
【題目】如圖,已知圓柱![]() ,底面半徑為1,高為2,
,底面半徑為1,高為2,![]() 是圓柱的一個(gè)軸截面,動(dòng)點(diǎn)
是圓柱的一個(gè)軸截面,動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿著圓柱的側(cè)面到達(dá)點(diǎn)
出發(fā)沿著圓柱的側(cè)面到達(dá)點(diǎn)![]() ,其路徑最短時(shí)在側(cè)面留下的曲線記為
,其路徑最短時(shí)在側(cè)面留下的曲線記為![]() :將軸截面
:將軸截面![]() 繞著軸
繞著軸![]() ,逆時(shí)針旋轉(zhuǎn)
,逆時(shí)針旋轉(zhuǎn)![]()
![]() 角到
角到![]() 位置,邊
位置,邊![]() 與曲線
與曲線![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
(1)當(dāng)![]() 時(shí),求證:直線
時(shí),求證:直線![]() 平面
平面![]() ;
;
(2)當(dāng)![]() 時(shí),求二面角
時(shí),求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)法一:建立如圖所示的空間直角坐標(biāo)系,寫出各點(diǎn)坐標(biāo),求得平面![]() 的法向量,可得結(jié)論;
的法向量,可得結(jié)論;
法二:由已知條件推導(dǎo)出AB⊥A1B1,AB⊥OO1,得到AB⊥平面A1B1C1D1,可得AB⊥B1D1,結(jié)合OP⊥B1D1由此能證明直線B1D1⊥平面PAB.
(2)以![]() 所在直線為
所在直線為![]() 軸,過點(diǎn)
軸,過點(diǎn)![]() 與
與![]() 垂直的直線為
垂直的直線為![]() 軸,
軸,![]() 所在的直線為
所在的直線為![]() 軸建立空間直角坐標(biāo)系,分別求得兩個(gè)面的法向量,利用向量法能求出二面角D﹣AB﹣P的余弦值.
軸建立空間直角坐標(biāo)系,分別求得兩個(gè)面的法向量,利用向量法能求出二面角D﹣AB﹣P的余弦值.
(1)方法一:當(dāng)![]() 時(shí),建立如圖所示的空間直角坐標(biāo)系,
時(shí),建立如圖所示的空間直角坐標(biāo)系,
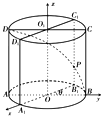
則有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() .
.
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,
,
可取![]() ,得
,得![]() ,
,![]() ,
,![]() .
.
所以直線![]() 平面
平面![]() .
.
方法二:在正方形![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
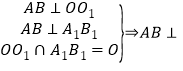 平面
平面![]() ,又
,又![]() 平面
平面![]()
所以![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]()
所以直線![]() 平面
平面![]() .
.
(2)當(dāng)![]() 時(shí),以
時(shí),以![]() 所在直線為
所在直線為![]() 軸,過點(diǎn)
軸,過點(diǎn)![]() 與
與![]() 垂直的直線為
垂直的直線為![]() 軸,
軸,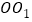 所在的直線為
所在的直線為![]() 軸建立如圖空間直角坐標(biāo)系,
軸建立如圖空間直角坐標(biāo)系,![]()
可得![]() ,所以
,所以![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則
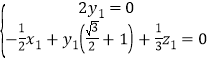 ,可取
,可取![]() ,得
,得![]() ,
,
又平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,則
,則![]()
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 同步練習(xí)河南大學(xué)出版社系列答案
同步練習(xí)河南大學(xué)出版社系列答案 同步練習(xí)西南師范大學(xué)出版社系列答案
同步練習(xí)西南師范大學(xué)出版社系列答案 補(bǔ)充習(xí)題江蘇系列答案
補(bǔ)充習(xí)題江蘇系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為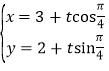 (其中
(其中![]() 為參數(shù)).以坐標(biāo)原點(diǎn)
為參數(shù)).以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系,并取相同的單位長(zhǎng)度,曲線
軸正半軸為極軸建立極坐標(biāo)系,并取相同的單位長(zhǎng)度,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)過點(diǎn)![]() 作直線
作直線![]() 的垂線交曲線
的垂線交曲線![]() 于
于![]() 兩點(diǎn),求
兩點(diǎn),求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以原點(diǎn)
為參數(shù)).以原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸為非負(fù)半軸為極軸建立極坐標(biāo)系,兩坐標(biāo)系相同的長(zhǎng)度單位.圓
軸為非負(fù)半軸為極軸建立極坐標(biāo)系,兩坐標(biāo)系相同的長(zhǎng)度單位.圓![]() 的方程為
的方程為![]() 被圓
被圓![]() 截得的弦長(zhǎng)為
截得的弦長(zhǎng)為![]() .
.
(Ⅰ)求實(shí)數(shù)![]() 的值;
的值;
(Ⅱ)設(shè)圓![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,若點(diǎn)
,若點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
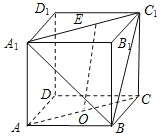
【題目】在正方體ABCD﹣A1B1C1D1中,O為線段AC的中點(diǎn),點(diǎn)E在線段A1C1上,則直線OE與平面A1BC1所成角的正弦值的取值范圍是( )
A.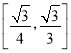 B.
B.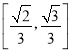 C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國(guó)剪紙是一種用剪刀或刻刀在紙上剪刻花紋,用于裝點(diǎn)生活或配合其他民俗活動(dòng)的民間藝術(shù);蘊(yùn)含了極致的數(shù)學(xué)美和豐富的傳統(tǒng)文化信息,現(xiàn)有一幅剪紙的設(shè)計(jì)圖,其中的4個(gè)小圓均過正方形的中心,且內(nèi)切于正方形的兩鄰邊.若在正方形內(nèi)隨機(jī)取一點(diǎn),則該點(diǎn)取自黑色部分的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著科技的發(fā)展,近年看電子書的國(guó)人越來越多;所以近期有許多人呼呼“回歸紙質(zhì)書”,目前出版物閱讀中紙質(zhì)書占比出現(xiàn)上升現(xiàn)隨機(jī)選出200人進(jìn)行采訪,經(jīng)統(tǒng)計(jì)這200人中看紙質(zhì)書的人數(shù)占總?cè)藬?shù)![]() .將這200人按年齡分成五組:第l組
.將這200人按年齡分成五組:第l組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,其中統(tǒng)計(jì)看紙質(zhì)書的人得到的頻率分布直方圖如圖所示.
,其中統(tǒng)計(jì)看紙質(zhì)書的人得到的頻率分布直方圖如圖所示.
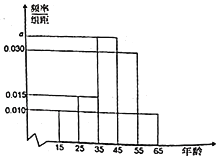
(1)求![]() 的值及看紙質(zhì)書的人的平均年齡;
的值及看紙質(zhì)書的人的平均年齡;
(2)按年齡劃分,把年齡在![]() 的稱青壯年組,年齡在
的稱青壯年組,年齡在![]() 的稱為中老年組,若選出的200人中看電子書的中老年人有10人,請(qǐng)完成下面
的稱為中老年組,若選出的200人中看電子書的中老年人有10人,請(qǐng)完成下面![]() 列聯(lián)表,并判斷能否在犯錯(cuò)誤的概率不超過0.1的前提下認(rèn)為看書方式與年齡層有關(guān)?
列聯(lián)表,并判斷能否在犯錯(cuò)誤的概率不超過0.1的前提下認(rèn)為看書方式與年齡層有關(guān)?
看電子書 | 看紙質(zhì)書 | 合計(jì) | |
青壯年 | |||
中老年 | |||
合計(jì) |
附:![]() (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知?jiǎng)訄A![]() 與
與![]() 軸相切,且與圓
軸相切,且與圓![]() :
:![]() 外切;
外切;
(1)求動(dòng)圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若直線![]() 過定點(diǎn)
過定點(diǎn)![]() ,且與軌跡
,且與軌跡![]() 交于
交于![]() 、
、![]() 兩點(diǎn),與圓
兩點(diǎn),與圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),若點(diǎn)
兩點(diǎn),若點(diǎn)![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求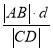 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,以坐標(biāo)原點(diǎn)為極點(diǎn),
中,以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(I)若![]() 為曲線
為曲線![]() 上的動(dòng)點(diǎn),點(diǎn)
上的動(dòng)點(diǎn),點(diǎn)![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點(diǎn)
,求點(diǎn)![]() 的軌跡
的軌跡![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù),![]() ,且直線
,且直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com