
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(I)若![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ,且直線
,且直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點到其準線的距離為
的焦點到其準線的距離為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)設直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 兩點,問拋物線
兩點,問拋物線![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 是正三角形?若存在,求出點
是正三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓柱![]() ,底面半徑為1,高為2,
,底面半徑為1,高為2,![]() 是圓柱的一個軸截面,動點
是圓柱的一個軸截面,動點![]() 從點
從點![]() 出發沿著圓柱的側面到達點
出發沿著圓柱的側面到達點![]() ,其路徑最短時在側面留下的曲線記為
,其路徑最短時在側面留下的曲線記為![]() :將軸截面
:將軸截面![]() 繞著軸
繞著軸![]() ,逆時針旋轉
,逆時針旋轉![]()
![]() 角到
角到![]() 位置,邊
位置,邊![]() 與曲線
與曲線![]() 相交于點
相交于點![]() .
.
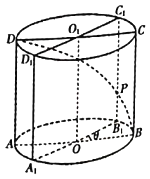
(1)當![]() 時,求證:直線
時,求證:直線![]() 平面
平面![]() ;
;
(2)當![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左、右頂點分別為
,左、右頂點分別為![]() 、
、![]() ,過左焦點的直線
,過左焦點的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點(異于
兩點(異于![]() 、
、![]() 兩點),當直線
兩點),當直線![]() 垂直于
垂直于![]() 軸時,四邊形
軸時,四邊形![]() 的面積為6.
的面積為6.
(1)求橢圓的方程;
(2)設直線![]() 、
、![]() 的交點為
的交點為![]() ;試問
;試問![]() 的橫坐標是否為定值?若是,求出定值;若不是,請說明理由.
的橫坐標是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,點
,點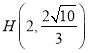 在橢圓上.
在橢圓上.
(Ⅰ)求橢圓的方程;
(Ⅱ)點![]() 在圓
在圓![]() 上,且
上,且![]() 在第一象限,過
在第一象限,過![]() 作
作![]() 的切線交橢圓于
的切線交橢圓于![]() 兩點,問:
兩點,問: ![]() 的周長是否為定值?若是,求出定值;若不是,說明理由.
的周長是否為定值?若是,求出定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
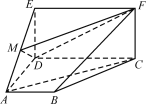
【題目】如圖,四邊形ABCD是梯形,四邊形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90,![]() ,M是線段AE上的動點.
,M是線段AE上的動點.
(1)試確定點M的位置,使AC∥平面DMF,并說明理由;
(2)在(1)的條件下,求平面MDF將幾何體ADE-BCF分成的兩部分的體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)不僅是著名的物理學家,也是著名的數學家,他利用“逼近法”得到橢圓的面積除以圓周率
年)不僅是著名的物理學家,也是著名的數學家,他利用“逼近法”得到橢圓的面積除以圓周率![]() 等于橢圓的長半軸與短半軸的乘積.已知平面直角坐標系
等于橢圓的長半軸與短半軸的乘積.已知平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]()
![]() 的面積為
的面積為![]() ,兩焦點與短軸的一個頂點構成等邊三角形.
,兩焦點與短軸的一個頂點構成等邊三角形.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 的直線
的直線![]() 與
與![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如下圖,漢諾塔問題是指有3根桿子A,B,C.B桿上有若干碟子,把所有碟子從B桿移到A桿上,每次只能移動一個碟子,大的碟子不能疊在小的碟子上面.把B桿上的4個碟子全部移到A桿上,最少需要移動( )次. ( )
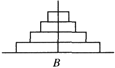
A.12 B.15 C.17 D.19
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com