(理)(本題滿分14分)如圖,已知直線
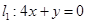
,直線
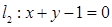
以及
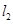
上一點
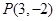
.
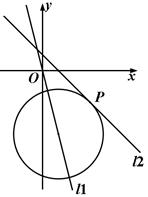
(Ⅰ)求圓心M在
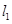
上且與直線
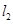
相切于點
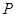
的圓⊙M的方程.
(Ⅱ)在(Ⅰ)的條件下;若直線
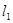
分別與直線
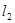
、圓⊙依次相交于
A、
B、
C三點,
求證:
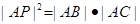
.
(1)

(2)利用切割線定理來證明。
試題分析:(解)(Ⅰ)設圓心為

,半徑為
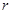
,依題意,


. ………………2分
設直線
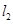
的斜率

,過
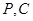
兩點的直線斜率
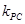
,因

,
故
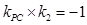
,
∴
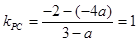
,……4分
解得
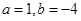
.
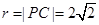
.……6分
所求圓的方程為

.……7分
(Ⅱ)聯(lián)立

則A

則

…….……9分
圓心

,

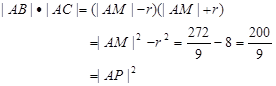
…….……13分
所以

得到驗證 . …….………….……14分
點評:解決該試題的關鍵是對于圓的方程的求解,一般采用 方法就是確定出圓心坐標,以及圓的半徑即可,然后利用題目中的條件表示出求解,同時圓與直線相切的時候,切割線定理的運用也是值得關注的一點。屬于中檔題。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
若點
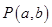
在圓C:
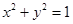
的外部,則直線
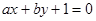
與圓C的位置關系是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知直線

:


為參數(shù)),圓

(極軸與

軸的非負半軸重合,且單位長度相同)。
⑴求圓心

到直線

的距離;
⑵若直線

被圓

截的弦長為

,求

的值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
過點A(1, -1),B(-1,1),且圓心在直線

上的圓的方程是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知圓C的半徑為

,圓心在直線

上,且被直線

截得的弦長為

,求圓C的方程
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分10分)
如圖,已知
C、
F是以
AB為直徑的半圓

上的兩點,且
CF=
CB,過
C作
CD^
AF交
AF的延長線與點
D.

(Ⅰ)證明:
CD為圓
O的切線;
(Ⅱ)若
AD=3,
AB=4,求
AC的長.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知以點

為圓心的圓與直線

相切.過點

的動直線

與圓

相交于

兩點,

是

的中點.

(1)求圓

的方程;
(2)當

時,求直線

的方程.(用一般式表示)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分10分)選修4-4:坐標系與參數(shù)方程
已知曲線
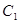
的極坐標方程是
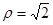
,曲線
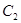
的參數(shù)方程是
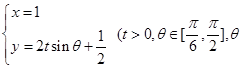
是參數(shù)).
(1)寫出曲線
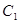
的直角坐標方程和曲線
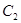
的普通方程;
(2)求
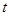
的取值范圍,使得
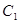
,
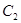
沒有公共點.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)在直角坐標系xOy中,曲線C1的點均在C2:(x-5)2+y2=9外,且對C1上任意一點M,M到直線x=﹣2的距離等于該點與圓C2上點的距離的最小值.
(1)求曲線C1的方程;
(2)設P(x0,y0)(y0≠±3)為圓C2外一點,過P作圓C2的兩條切線,分別與曲線C1相交于
點A,B和C,D.證明:當P在直線x=﹣4上運動時,四點A,B,C,D的縱坐標之積為定值.
查看答案和解析>>

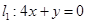 ,直線
,直線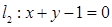 以及
以及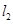 上一點
上一點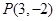 .
.
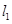 上且與直線
上且與直線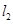 相切于點
相切于點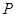 的圓⊙M的方程.
的圓⊙M的方程.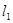 分別與直線
分別與直線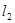 、圓⊙依次相交于A、B、C三點,
、圓⊙依次相交于A、B、C三點,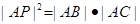 .
.  :
:
 為參數(shù)),圓
為參數(shù)),圓 (極軸與
(極軸與 軸的非負半軸重合,且單位長度相同)。
軸的非負半軸重合,且單位長度相同)。 到直線
到直線 的距離;
的距離; 被圓
被圓 截的弦長為
截的弦長為 ,求
,求 的值。
的值。 上的兩點,且CF=CB,過C作CD^AF交AF的延長線與點D.
上的兩點,且CF=CB,過C作CD^AF交AF的延長線與點D.
 為圓心的圓與直線
為圓心的圓與直線 相切.過點
相切.過點 的動直線
的動直線 與圓
與圓 相交于
相交于 兩點,
兩點, 是
是 的中點.
的中點.
 的方程;
的方程;  時,求直線
時,求直線 的方程.(用一般式表示)
的方程.(用一般式表示)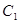 的極坐標方程是
的極坐標方程是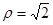 ,曲線
,曲線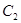 的參數(shù)方程是
的參數(shù)方程是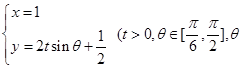 是參數(shù)).
是參數(shù)).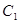 的直角坐標方程和曲線
的直角坐標方程和曲線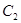 的普通方程;
的普通方程;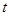 的取值范圍,使得
的取值范圍,使得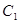 ,
,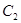 沒有公共點.
沒有公共點.