
本題滿分10分)
設函數
 為奇函數,其圖象在點
為奇函數,其圖象在點 處的切線與直線
處的切線與直線 垂直,導函數
垂直,導函數 的最小值為
的最小值為 .試求
.試求 ,
, ,
, 的值。
的值。
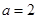 ,
,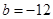 ,
,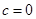 .
.
【解析】
試題分析:由y=f(x)為奇函數,知c=0,故f(x)=ax3+bx,所以f'(x)=3ax2+b,f'(1)=3a+b=-6,由導數f'(x)的 最小值為-12,知b=-12,由此能求出a,b,c的值.
解:∵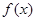 為奇函數,∴
為奇函數,∴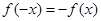
即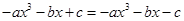 ∴
∴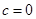 (4分)
(4分)
∵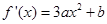 的最小值為
的最小值為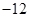 ∴
∴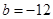 (6分)
(6分)
又直線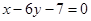 的斜率為
的斜率為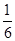 因此,
因此, (8分)
(8分)
∴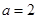 ,
,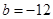 ,
,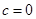 .(10分)
.(10分)
考點:本題主要考查了導數的性質和應用,是基礎題.解題時要認真審題,仔細解答,注意合理地進行等價轉化.
點評:解決該試題的關鍵是理解導數幾何意義的運用明確導數的值即為該點處的切線的斜率,只要只要點的坐標和導數值,既可以寫出切線方程。


科目:高中數學 來源:2012屆浙江省臺州中學高三上學期第一次統練理科數學 題型:解答題
(本題滿分10分)設函數 ,
,
(1)若函數 在
在 處與直線
處與直線 相切;
相切;
①求實數 的值;②求函數
的值;②求函數 上的最大值;
上的最大值;
(2)當 時,若不等式
時,若不等式 對所有的
對所有的 都成立,求實數
都成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年遼寧沈陽二中等重點中學協作體高三領航高考預測(二)文數學卷(解析版) 題型:解答題
(本題滿分10分)設函數 .
.
(1)畫出函數y=f(x)的圖像;
(2)若不等式 ,(a¹0,a、bÎR)恒成立,求實數x的范圍.
,(a¹0,a、bÎR)恒成立,求實數x的范圍.
查看答案和解析>>
科目:高中數學 來源:2013屆湖北省仙桃市高二下學期期中考試理科數學試卷(解析版) 題型:解答題
(本題滿分10分)
設函數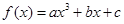
 為奇函數,其圖象在點
為奇函數,其圖象在點 處的切線與直線
處的切線與直線 垂直,導函數
垂直,導函數 的最小值為
的最小值為 .試求
.試求 ,
, ,
, 的值。
的值。
查看答案和解析>>
科目:高中數學 來源:2010-2011年河北省高二下學期期末考試理科數學 題型:解答題
(本題滿分10分)設 的內角A、B、C所對的邊長分別為
的內角A、B、C所對的邊長分別為 ,且
,且 ,
, 。
。
(1)當 時,求
時,求 的值.
的值.
(2)當 的面積為3時,求
的面積為3時,求 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com