
已知 且
且 ,
, ,當
,當 時
時 恒成立,則實數
恒成立,則實數 的取值范圍
的取值范圍 .
.
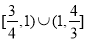
【解析】
試題分析:轉化為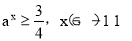 上恒成立,再分類討論最小值恒大于或等于
上恒成立,再分類討論最小值恒大于或等于 ,求解即可.
,求解即可.
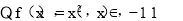 ∴f(x)∈[0,1),∵f(x)<g(x)恒成立,∴只需g(x)≥1即可.
∴f(x)∈[0,1),∵f(x)<g(x)恒成立,∴只需g(x)≥1即可.
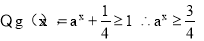 x∈(-1,1)上恒成立,
x∈(-1,1)上恒成立,
當a>1時,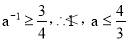 當0<a<1時,
當0<a<1時,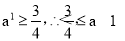
故實數a的取值范圍為: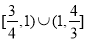
考點:指數函數單調性的應用.


科目:高中數學 來源:2014-2015學年黑龍江省高一上第一次月考數學試卷(解析版) 題型:解答題
(本小題滿分10分)設全集 ,集合
,集合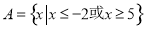 ,
, .
.
求:(1) ;
;
(2)記 ,
, ,且
,且 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省龍巖市高三上學期期末考試文科數學試卷(解析版) 題型:填空題
已知直線2x+y-4=0過橢圓E: 的右焦點F2,且與橢圓E在第一象限的交點為M,與y軸交于點N,F1是橢圓E的左焦點,且|MN|=|MF1|,則橢圓E的方程為 .
的右焦點F2,且與橢圓E在第一象限的交點為M,與y軸交于點N,F1是橢圓E的左焦點,且|MN|=|MF1|,則橢圓E的方程為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省高三高考壓軸文科數學試卷(解析版) 題型:解答題
如圖, ,
, 為圓柱
為圓柱 的母線,
的母線, 是底面圓
是底面圓 的直徑,
的直徑, ,
, 分別是
分別是 ,
, 的中點,
的中點, .
.
(1)證明: ;
;
(2)證明: ;
;
(3)假設這是個大容器,有條體積可以忽略不計的小魚能在容器的任意地方游弋,如果魚游到四棱錐 內會有被捕的危險,求魚被捕的概率.
內會有被捕的危險,求魚被捕的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com