
【題目】某中學(xué)調(diào)查了某班全部![]() 名同學(xué)參加書法社團和演講社團的情況,數(shù)據(jù)如下表:(單位:人)
名同學(xué)參加書法社團和演講社團的情況,數(shù)據(jù)如下表:(單位:人)

(1)能否由![]() 的把握認為參加書法社團和參加演講社團有關(guān)?
的把握認為參加書法社團和參加演講社團有關(guān)?
(附: 
當(dāng)![]() 時,有
時,有![]() 的把握說事件
的把握說事件![]() 與
與![]() 有關(guān);當(dāng)
有關(guān);當(dāng)![]() ,認為事件
,認為事件![]() 與
與![]() 是無關(guān)的)
是無關(guān)的)
(2)已知既參加書法社團又參加演講社團的![]() 名同學(xué)中,有
名同學(xué)中,有![]() 名男同學(xué)
名男同學(xué)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 名女同學(xué)
名女同學(xué)![]() ,
, ![]() ,
, ![]() .現(xiàn)從這
.現(xiàn)從這![]() 名男同學(xué)和
名男同學(xué)和![]() 名女同學(xué)中各隨機選
名女同學(xué)中各隨機選![]() 人,求
人,求![]() 被選中且
被選中且![]() 未被選中的概率.
未被選中的概率.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)將列聯(lián)表中的數(shù)據(jù)代入公式 ,可求得
,可求得![]() ,與鄰界值比較,即可得到結(jié)論;(2)利用列舉法,確定基本事件從這
,與鄰界值比較,即可得到結(jié)論;(2)利用列舉法,確定基本事件從這![]() 名男同學(xué)和
名男同學(xué)和![]() 名女同學(xué)中各隨機選
名女同學(xué)中各隨機選![]() 人的個數(shù)為
人的個數(shù)為![]() ,以及事件“
,以及事件“![]() 被選中且
被選中且![]() 未被選中”所包含的基本事件有
未被選中”所包含的基本事件有![]() 個,利用古典概型概率公式可求出
個,利用古典概型概率公式可求出![]() 被選中且
被選中且![]() 未被選中的概率.
未被選中的概率.
試題解析:(1)由調(diào)查數(shù)據(jù)可知,![]()
沒有![]() 的把握認為參加書法社團和參加演講社團有關(guān).
的把握認為參加書法社團和參加演講社團有關(guān).
(2)從這![]() 名男同學(xué)和
名男同學(xué)和![]() 名女同學(xué)中各隨機選
名女同學(xué)中各隨機選![]() 人,其一切可能的結(jié)果組成的基本事件有:
人,其一切可能的結(jié)果組成的基本事件有:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共
共![]() 個.
個.
根據(jù)題意,這些基本事件的出現(xiàn)是等可能的.
事件“![]() 被選中且
被選中且![]() 未被選中”所包含的基本事件有:
未被選中”所包含的基本事件有: ![]() ,
, ![]() ,共
,共![]() 個.
個.
因此, ![]() 被選中且
被選中且![]() 為被選中的概率為
為被選中的概率為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求曲線![]() 在點處的切線方程;
在點處的切線方程;
(Ⅱ)當(dāng)![]() 時,求證:函數(shù)
時,求證:函數(shù)![]() 有且僅有一個零點;
有且僅有一個零點;
(Ⅲ)當(dāng)![]() 時,寫出函數(shù)
時,寫出函數(shù)![]() 的零點的個數(shù).(只需寫出結(jié)論)
的零點的個數(shù).(只需寫出結(jié)論)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,,其中
,,其中![]() .
.
(I)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)證明: ![]() 在區(qū)間
在區(qū)間![]() 上恰有2個零點.
上恰有2個零點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 上的兩個動點
上的兩個動點![]() ,
, ![]() 的橫坐標(biāo)
的橫坐標(biāo)![]() ,線段
,線段![]() 的中點坐標(biāo)為
的中點坐標(biāo)為![]() ,直線
,直線![]() 與線段
與線段![]() 的垂直平分線相交于點
的垂直平分線相交于點![]() .
.
(1)求點![]() 的坐標(biāo);
的坐標(biāo);
(2)求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列![]() 滿足
滿足![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.
(1)求數(shù)列![]() 和
和![]() 的通項公式;
的通項公式;
(2)數(shù)列![]() 滿足
滿足![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中, ![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,
的中點, ![]() ,
, ![]() .
.
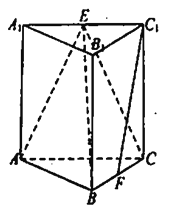
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩家外賣公司,其送餐員的日工資方案如下:甲公司的底薪80元,每單抽成4元;乙公司無底薪,40單以內(nèi)(含40單)的部分每單抽成6元,超出40單的部分每單抽成7元,假設(shè)同一公司送餐員一天的送餐單數(shù)相同,現(xiàn)從兩家公司各隨機抽取一名送餐員,并分別記錄其50天的送餐單數(shù),得到如下頻數(shù)表:
甲公司送餐員送餐單數(shù)頻數(shù)表
送餐單數(shù) | 38 | 39 | 40 | 41 | 42 |
天數(shù) | 10 | 15 | 10 | 10 | 5 |
乙公司送餐員送餐單數(shù)頻數(shù)表
送餐單數(shù) | 38 | 39 | 40 | 41 | 42 |
天數(shù) | 5 | 10 | 10 | 20 | 5 |
(1)現(xiàn)從甲公司記錄的50天中隨機抽取3天,求這3天送餐單數(shù)都不小于40的概率;
(2)若將頻率視為概率,回答下列兩個問題:
①記乙公司送餐員日工資為![]() (單位:元),求
(單位:元),求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
②小王打算到甲、乙兩家公司中的一家應(yīng)聘送餐員,如果僅從日工資的角度考慮,請利用所學(xué)的統(tǒng)計學(xué)知識為小王作出選擇,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
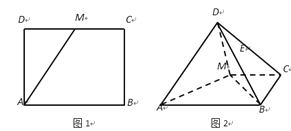
【題目】長方形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 中點(圖1).將△
中點(圖1).將△![]() 沿
沿![]() 折起,使得
折起,使得![]() (圖2)在圖2中:
(圖2)在圖2中:
(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存點
上是否存點![]() ,使得二面角
,使得二面角![]() 為大小為
為大小為![]() ,說明理由.
,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
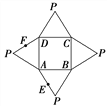
【題目】如圖是一幾何體的平面展開圖,其中ABCD為正方形,E,F分別為PA,PD的中點,
在此幾何體中,給出下面四個結(jié)論:
①直線BE與直線CF異面; ②直線BE與直線AF異面;
③直線EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com