
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)討論函數![]() 的單調性;
的單調性;
(2)函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點,
兩點, ![]() ,點
,點![]() 在函數
在函數![]() 的圖象上,且
的圖象上,且![]() 為等腰直角三角形,記
為等腰直角三角形,記 ,求
,求![]() 的值.
的值.
【答案】(1)見解析(2)見解析
【解析】試題分析:(1)對函數求導,利用導數與函數單調性的關系,對![]() 進行分類討論可得結果;(2)由函數圖象交
進行分類討論可得結果;(2)由函數圖象交![]() 軸于兩點,兩點橫坐標滿足方程.又根據直角三角斜邊的中線性質可得
軸于兩點,兩點橫坐標滿足方程.又根據直角三角斜邊的中線性質可得![]() 三者間關系,最后利用
三者間關系,最后利用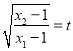 將方程轉化成只含有
將方程轉化成只含有![]() 兩個變量,可求得兩變量關系,進一步求得
兩個變量,可求得兩變量關系,進一步求得![]() 的值.試題解析:
的值.試題解析:
(Ⅰ)![]() .
.
①當![]() 時,則
時,則![]() ,則函數
,則函數![]() 在
在![]() 是單調增函數.
是單調增函數.
②當![]() 時,令
時,令![]() ,則
,則![]() ,
,
若![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上是單調減函數;
上是單調減函數;
若![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上是單調增函數.
上是單調增函數.
(Ⅱ)由(Ⅰ)可知當![]() 時,函數
時,函數![]() 其圖象與
其圖象與![]() 軸交于兩點,則有
軸交于兩點,則有![]() ,則
,則![]()
![]()
![]() .
.
于是![]() ,在等腰三角形ABC中,顯然C = 90°,所以
,在等腰三角形ABC中,顯然C = 90°,所以![]() ,即
,即![]() ,
,
由直角三角形斜邊的中線性質,可知![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() .
.
因為![]() ,則
,則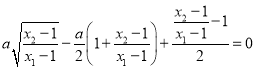 ,
,
又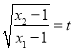 ,所以
,所以![]() ,
,
即![]() ,則
,則![]() 所以
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】某服裝廠生產一種服裝,每件服裝的成本為40元,出廠單價定為60元,該廠為鼓勵銷售商訂購,決定當一次訂購量超過100件時,每多訂購一件,訂購的全部服裝的出場單價就降低0.02元,根據市場調查,銷售商一次訂購量不會超過600件.
(1)設一次訂購x件,服裝的實際出廠單價為p元,寫出函數p=f(x)的表達式;
(2)當銷售商一次訂購多少件服裝時,該廠獲得的利潤最大?其最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】f(x)是定義在R上的函數,且對任意的x、y都有f(x+y)=f(x)+f(y)﹣1成立.當x>0時,f(x)>1.
(1)若f(4)=5,求f(2);
(2)證明:f(x)在R上是增函數;
(3)若f(4)=5,解不等式f(3m2﹣m﹣2)<3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,則關于函數F(x)=f(f(x))的零點個數,正確的結論是 . (寫出你認為正確的所有結論的序號)
,則關于函數F(x)=f(f(x))的零點個數,正確的結論是 . (寫出你認為正確的所有結論的序號)
①k=0時,F(x)恰有一個零點.②k<0時,F(x)恰有2個零點.
③k>0時,F(x)恰有3個零點.④k>0時,F(x)恰有4個零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在統計學中,偏差是指個別測定值與測定的平均值之差,在成績統計中,我們把某個同學的某科考試成績與該科班平均分的差叫某科偏差,班主任為了了解個別學生的偏科情況,對學生數學偏差![]() (單位:分)與物理偏差
(單位:分)與物理偏差![]() (單位:分)之間的關系進行學科偏差分析,決定從全班56位同學中隨機抽取一個容量為8的樣本進行分析,得到他們的兩科成績偏差數據如下:
(單位:分)之間的關系進行學科偏差分析,決定從全班56位同學中隨機抽取一個容量為8的樣本進行分析,得到他們的兩科成績偏差數據如下:
學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
數學偏差 | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差 | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知![]() 與
與![]() 之間具有線性相關關系,求
之間具有線性相關關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若這次考試該班數學平均分為118分,物理平均分為90.5,試預測數學成績126分的同學的物理成績.
參考公式: 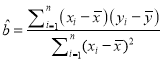 ,
, ![]() ,
,
參考數據: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著生活水平的提高,人們對空氣質量的要求越來越高,某機構為了解公眾對“車輛限行”的態度,隨機抽查![]() 人,并將調查情況進行整理后制成下表:
人,并將調查情況進行整理后制成下表:
年齡(歲) |
|
|
|
|
|
頻數 |
|
|
|
|
|
贊成人數 |
|
|
|
|
|
(1)世界聯合國衛生組織規定: ![]() 歲為青年,
歲為青年, ![]() 為中年,根據以上統計數據填寫以下
為中年,根據以上統計數據填寫以下![]() 列聯表:
列聯表:
青年人 | 中年人 | 合計 | |
不贊成 | |||
贊成 | |||
合計 |
(2)判斷能否在犯錯誤的概率不超過![]() 的前提下,認為贊成“車柄限行”與年齡有關?
的前提下,認為贊成“車柄限行”與年齡有關?
附: 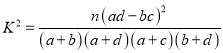 ,其中
,其中![]()
獨立檢驗臨界值表:
|
|
|
|
|
|
|
|
|
|
(3)若從年齡![]() 的被調查中各隨機選取
的被調查中各隨機選取![]() 人進行調查,設選中的兩人中持不贊成“車輛限行”態度的人員為
人進行調查,設選中的兩人中持不贊成“車輛限行”態度的人員為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為0的等差數列{an}滿足:a1=1且a2 , a5 , a14成等比數列.
(1)求數列{an}的通項公式an和前n項和Sn;
(2)證明不等式 ![]() 且n∈N*)
且n∈N*)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的二次函數f(x)=ax2﹣4bx+1
(Ⅰ)設集合P={1,2,3},集合Q={﹣1,1,2,3,4},從集合P中隨機取一個數作為a,從集合Q中隨機取一個數作為b,求函數f(x)在區間[1,+∞)上是增函數的概率;
(Ⅱ)設點(a,b)是區域 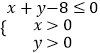 內的隨機點,求函數f(x)在區間[1,+∞)上是增函數的概率.
內的隨機點,求函數f(x)在區間[1,+∞)上是增函數的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com