
分析 (1)由正弦定理即可求出C的大小,再根據正弦定理和兩角和的正弦公式即可求出b
(2)根據正弦定理、商的關系化簡已知的式子,由條件和誘導公式求出B-A的值,求出C和A的范圍,由誘導公式和二倍角的余弦公式變形化簡,利用換元法和二次函數的性質求出式子的范圍.
解答 解:(1)由正弦定理可得$\frac{c}{sinC}$=$\frac{a}{sinA}$,
∵c=$\sqrt{6},A={45°}$,a=2,
∴sinC=$\frac{\sqrt{6}×\frac{\sqrt{2}}{2}}{2}$=$\frac{\sqrt{3}}{2}$,
∴C=60°或120°,
由正弦定理可得b=$\frac{asinB}{sinA}$
當C=60°,sinB=sin(A+C)=sin45°cos60°+cos45°sin60°=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴b=$\frac{2×\frac{\sqrt{6}+\sqrt{2}}{4}}{\frac{\sqrt{2}}{2}}$=1+$\sqrt{3}$,
當C=120°,sinB=sin(A+C)=sin45°cos120°+cos45°sin120°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
∴b=$\sqrt{3}$-1,
(2)由題意得a=btanA,
∴由正弦定理得sinA=sinB•$\frac{sinA}{cosA}$,則sinB=cosA,
∵B為鈍角,∴B=$\frac{π}{2}$+A,
∴B-A=$\frac{π}{2}$;
∴C=π-(A+B)=π-(A+$\frac{π}{2}$+A)=$\frac{π}{2}$-2A>0,
∴A∈(0,$\frac{π}{4}$),
∴sinA+sinC=sinA+sin($\frac{π}{2}$-2A)
=sinA+cos2A=sinA+1-2sin2A
=-2(sinA-$\frac{1}{4}$)2+$\frac{9}{8}$,
∵A∈(0,$\frac{π}{4}$),∴0<sinA<$\frac{\sqrt{2}}{2}$,
∴由二次函數可知,$\frac{\sqrt{2}}{2}$<-2(sinA-$\frac{1}{4}$)2+$\frac{9}{8}$≤$\frac{9}{8}$,
∴sinA+sinC的取值范圍為($\frac{\sqrt{2}}{2}$,$\frac{9}{8}$]
點評 本題考查三角函數中恒等變換的應用,正弦定理,以及換元法和二次函數的性質,熟練掌握公式和定理是解題的關鍵.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案科目:高中數學 來源: 題型:選擇題
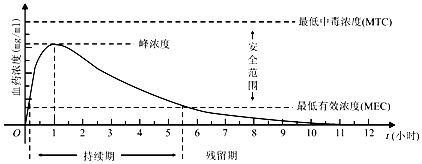
| A. | 首次服用該藥物1單位約10分鐘后,藥物發揮治療作用 | |
| B. | 每次服用該藥物1單位,兩次服藥間隔小于2小時,一定會產生藥物中毒 | |
| C. | 每間隔5.5小時服用該藥物1單位,可使藥物持續發揮治療作用 | |
| D. | 首次服用該藥物1單位3小時后,再次服用該藥物1單位,不會發生藥物中毒 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 日期 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 優惠金額x(千元) | 10 | 11 | 13 | 12 | 8 |
| 銷售量y(輛) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 《九章算術》是我國古代內容極為豐富的數學名著,書中有如下問題:“今有芻甍,下廣三丈,袤四丈,上袤二丈,無廣,高一丈.問積幾何?”其意思為:“今有底面為矩形的屋脊狀的楔體,下底面寬3丈,長4丈,上棱長2丈,無寬,高1丈.現給出該楔體的三視圖,其中網格紙上小正方形的邊長為1丈,則該楔體的體積為( )
《九章算術》是我國古代內容極為豐富的數學名著,書中有如下問題:“今有芻甍,下廣三丈,袤四丈,上袤二丈,無廣,高一丈.問積幾何?”其意思為:“今有底面為矩形的屋脊狀的楔體,下底面寬3丈,長4丈,上棱長2丈,無寬,高1丈.現給出該楔體的三視圖,其中網格紙上小正方形的邊長為1丈,則該楔體的體積為( )| A. | 4立方丈 | B. | 5立方丈 | C. | 6立方丈 | D. | 8立方丈 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com